Attention

This document was last updated Nov 25 24 at 21:59

ASIC Technology

Important

The purpose of this lecture is as follows.

  • Answer the questions: what is an ASIC? why do we need it? [slides]

  • To review the historical context of ASIC hardware design [Feynman, SIA]

  • To discuss new insight into the needs of ASIC hardware design [Leiserson, Henessy]

  • To get insight into the fundamental limits of scaling [Markov, Ruch]

Attention

The following references are relevant background to this lecture.

If history learns us anything ..

This course presents a modern view of the hardware design process, with specific attention to ASIC technology. Our goal is to understand what matters in modern hardware design. Over the past decades, hardware has undergone major, profound changes that deeply affect how modern hardware design works. We specifically consider ASIC design of digital hardware based on standard cell technology. This is just one target among many different variants (FPGA, sea-of-gates, full-custom hardware, etc.), but it likely dominates modern chip design. Furthermore, our observations for ASIC standard cell design will also apply, in many aspects, to design for other targets.

In this introductory lecture, we look at the past and attempt to explain the current state of hardware design.

Plenty of room at the bottom

A unique characteristic of digital hardware is that it is small, very small. One billion transistors on a chip is not uncommon nowadays, and the latest M4 processor of Apple has 28 billion transistors. That is a mind boggling number of devices, to be able to hold in one’s hand.

Hardware has not always been small. You may have seen images of room-filling computers, which were common in the first half of the 20th century and had the equivalent of a few thousand logical switches. From then to today, we have figured out how to scale the design process for hardware from 10,000 switches to 100 billion switches. That is an increase of 7 orders of magnitude! This required scaling down these former mechanical switches to infinitesimal sizes. The reason this scaling can be done at all is because the components of nature are also of infinitesimal size.

One of the first people to remind us of this feature was Prof. Richard P. Feynman, one of the greatest physicists of modern times. In 1959, he wrote a paper called There is Plenty of Room at the Bottom, which explores the physical limitations in nature toward building computers. His conclusions were essentially that most of the limitations in scaling were related to the engineering of small systems, not to the limitations that nature itself had imposed.

Printing Small

For example, Feynman goes through a thought experiment to print the entire Britannica, a 24-volume encyclopedia, on the head of a pin one-sixteenth of an inch in diameter. He concludes that this can be done by scaling down the printing by 25,000 times. So the question then is whether we can print a font small enough for it to be printed. The smallest feature of the Britannica is a grayscale dot one hundred-twentieth of an inch wide. Reducing that dot 25,000 times would leave a dot 80 Angstroms across—roughly 32 metal atoms. So the shrunken dot occupies just 1,000 atoms, and that would be the tiniest feature that has to be printed. He concludes, therefore, that the Britannica would physically fit on the head of a pin, and the only thing stopping us from doing it is the absence of a (1959) printing technology to provide such small printing features.

Feynman goes one step further by evaluating how much room would be needed to store all of human knowledge, estimated at 24 million books in 1959. Storing each bit in a cube of 5 by 5 by 5 atoms (so roughly 125 atoms per bit), he concludes that a cube one two-hundredth of an inch wide is sufficient to store 24 million books. Therefore, Feynman states that there is PLENTY of room at the bottom, not just room at the bottom.

Computing in the Small

The next question Feynman tackles is whether it’s possible to build machines that are very small. He points out that biology has excelled at building small machines. For example, humans have no trouble recognizing faces using a computer the size of a brain. Conversely, solving the same problem with 1959 technology would require an enormous computer, which would not only be very big but also a lot slower due to its enormous physical size.

However, Feynman points out that the limitations on small machines are set by engineering constraints. Any manufactured artifact is subject to manufacturing tolerances and may not have a homogeneous material structure. That puts hard limits on how small you can effectively build.

He further points out that scaling changes the nature of a design. For example, material becomes relatively stronger at a smaller scale, and some features start to change—such as the magnetism created by magnetic dipoles. As electric circuits are physically scaled down, their properties change. For example, their natural frequency increases significantly. Therefore, electric circuits may have to be redesigned when they are scaled down. But again, scaling only causes engineering challenges and does not pose physical limitations.

Feynman goes through a thought experiment on how to build such a small computer. He describes something that is amazingly similar to how modern chips are produced. He describes a mechanism where one large machine can make several smaller-size copies of itself. This process can be repeated several times to create smaller and smaller machines. All the while, this could be achieved by using roughly a constant amount of raw material because the machines become so much smaller. Recall that modern chip-making machines still use the principle of optical scaling to construct a miniature version of a machine in raw material.

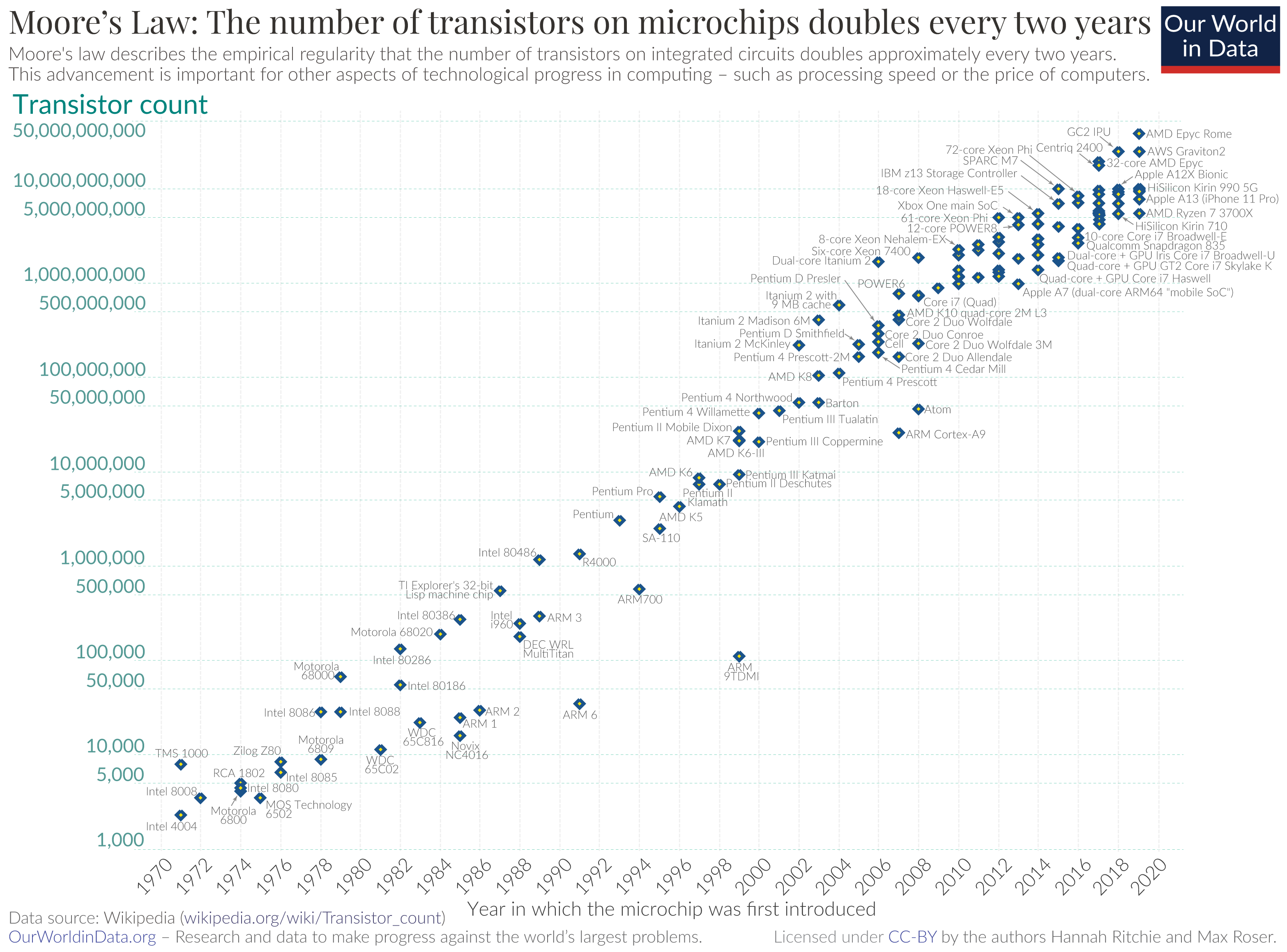
Moore’s law

The famous Moore’s Law, captured in a 1965 paper by Dr. Gordon Moore, observes that the number of transistors integrated on a chip doubles roughly every two years. In essence, Gordon Moore showed that Feynman’s observations are confirmed in practice. Scaling works because the engineering problems of scaling can be solved.

The amazing insight of Moore’s Law is that scaling works as well as it does. The following figure by Richie and Roser dramatically demonstrates just how much scaling Moore’s Law has provided: 7 orders of magnitude, and still, the scaling continues!

It’s fashionable to say that ‘Moore’s Law is dead’ or ‘ending,’ but the truth is that there has been nothing in engineering that has achieved the same level of efficiency. Compared to 50 years ago, does a car consume 7 orders of magnitude less fuel? No! Compared to 50 years ago, do we cover 7 orders of magnitude more topics in the engineering curriculum? No!

It is correct that the physical limits of scaling are real, and in this sense, Moore’s Law faces a wall. But engineers are never stopped by walls. Instead, they find a way around and continue.

_images/moore.png

Historically, there have been two breaking points in the race to put more components on a chip. The best-known breaking point is Moore’s Law. Another factor that has had an equal impact is Dennard’s scaling law, which was used until 2006 to decide how to adjust the supply voltage of transistors as they are shrunk smaller. The supply voltage of digital technology matters because it determines the maximum voltage that can occur across a gate’s source and drain when the gate is turned off, and it determines the peak current that can occur through the transistor when the gate switches on.

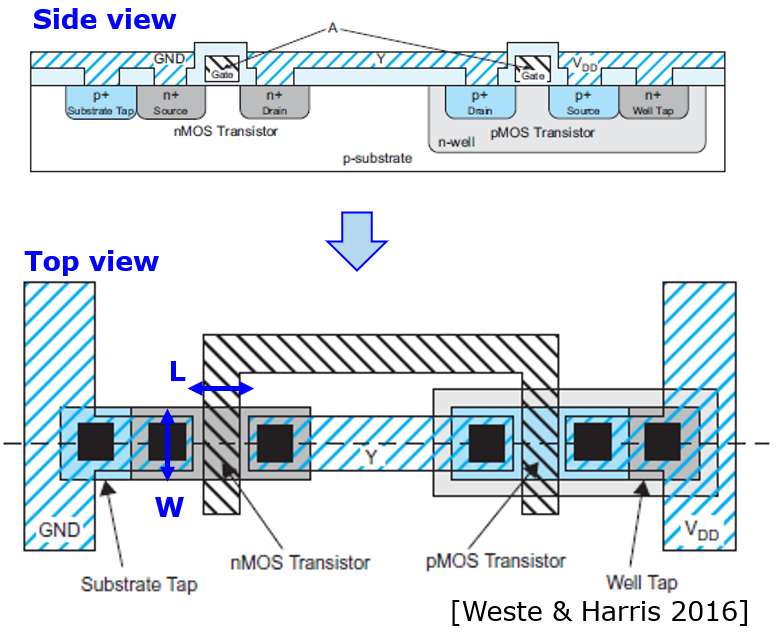
_images/inverterlayout.png

Before 2006, when Dennard’s scaling still applied, the following rules were used to drive scaling. When the dimension of the length L and width W each scale by a factor of 0.7, then the following holds:

  • The area of the transistor drops to half (resulting in twice as many transistors on the same die space).

  • The capacitance C of the transistor input scales by 0.7.

  • The voltage V across the transistor must be scaled by 0.7 to keep the electrical field within the transistor constant (excessive field strength can destroy the transistor).

  • The switching delay of the transistor scales by 0.7, as a smaller capacitance is switched across a smaller voltage, but with a smaller charging current.

  • The dynamic power consumption of the transistor reduces by half, as the dynamic power consumption is given by V^2 C f. Furthermore, because there are twice as many transistors in the same die area, the power density (power per unit of area) remains constant.

The beauty of Dennard scaling is that chips become faster and can carry more transistors with every generation. However, since 2006, the frequency no longer increases, and the voltage no longer decreases with every new technology generation. This was due to several reasons. First, Dennard scaling does not take static power consumption into account (transistor leakage current), which deteriorates the power density. Second, Dennard scaling does not take the delay through interconnect into account. Wires do not shrink in the same manner as transistors, making the interconnect delay play a more important role in each new scaled-down generation.

The impact of the end of Dennard Scaling on chip performance is considerable, as can be clearly seen in K. Rupp’s [chart of microprocessor data](https://www.karlrupp.net/2018/02/42-years-of-microprocessor-trend-data/).

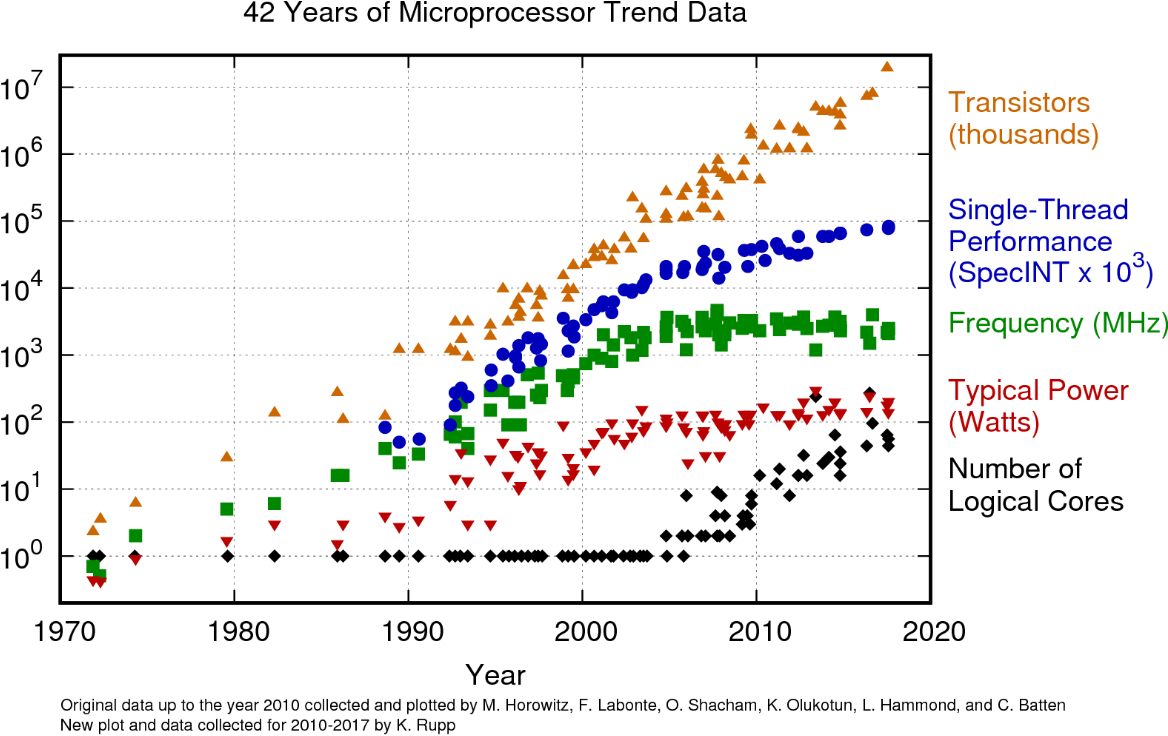
_images/ruppcpudata.png

We can clearly see that the number of transistors keeps increasing with every new generation (orange). But, since processors don’t run any faster (green), it becomes harder to get more instructions completed on a single processor (blue). One important trend to keep system performance growing is to increase the number of cores per chip (black).

And still, even this scaling story comes to an end because the scaling of transistors runs into physical limitations. Advanced process technologies are still able to shrink transistors, but it becomes very expensive to do so. As observed by several authors, the cost per transistor is no longer decreasing (for example, read [this post](https://www.fabricatedknowledge.com/p/the-rising-tide-of-semiconductor) by D. O’Loughlin on the rising cost of semiconductors). The implications of a constant transistor cost are not minor. Simply put, it no longer pays off to migrate a given system function to a smaller technology node. You can still get increased capacity by moving to a smaller technology node, but such a chip will be more expensive, too.

![End of Moore’s Law](img/endofmoore.png)

Slide by Marvell Semiconductor ([Marvell Investor Day Slide 43](https://filecache.investorroom.com/mr5ir_marvell/131/download/Marvell%20Investor%20Day%202020.pdf))

And hence, we must revise how digital systems are built. This is a very profound change with implications at every level of abstraction. Indeed, the only way to make hardware systems faster is to make every transistor perform more efficiently. Throwing more transistors at a problem is no longer a catch-all solution because more transistors also cost more.

Plenty of room at the top

Intel had 14nm chips in 2014 and then stalled on 10nm integration in 2016, delaying its use to 2019. Increasingly, the scaling-down process becomes more difficult, and to keep building better hardware and better computers, we will need to build better computers. The following discussion is limited to improvements that can be made using traditional computing techniques and does not consider alternative computing mechanisms such as quantum computing.

The problem of building better computers (and not just smaller computers) is captured by Dr. Charles Leiserson and his colleagues in a paper called Plenty of Room at the Top. He observes that, to compensate for the increased difficulty in scaling, innovation is needed in three areas: better software, better algorithms, and better hardware architecture.

Better software

Leiserson observes that the efficiency of software (in terms of speed) varies by orders of magnitude in performance. Consider, for example, a matrix multiplication, which is typically expressed as a three-level loop:

for i in xrange(4096):
  for j in xrange(4096):
    for k in xrange(4096):
      C[i][j] += A[i][k] * B[k][j]

Depending on the programming environment, the execution time will greatly vary, even is the exact same hardware is utilized. The numbers provided in the paper tell it all:

Language

Rel. Speed

Rel. Speedup

Python

1

NA

Java

11

10.8

C

47

4.4

Parallel Loops

366

7.8

Parallel + Locality

6,727

18.4

  • Vectorization

23,224

3.5

  • AVX Instrinsix

62,806

2.7

The reason for this speedup across almost 5 orders of magnitude is due to several factors, such as (1) algorithmic improvements, (2) making sure that the problem becomes a better ‘fit’ for the hardware, and (3) ensuring that all the special features of hardware (e.g., vector instructions) are properly used. Another way of looking at this result is to say that the flexibility and generality of native Python come at an enormous efficiency overhead. As scaling becomes harder, the impact of this overhead is increasingly felt at higher layers of abstraction in the application stack. Therefore, the application must move ‘closer’ to the hardware to experience the same effect that Moore’s law provided for decades.

Dr. Leiserson uses the term software bloat to describe this inefficiency. He observes that this inefficiency is essentially caused by the common practice in software engineering to solve problems by reduction. This means the following: You have to solve problem A, but you already have a solution to solve problem B. Rather than building a computer to solve problem A, you figure out a technique to transform problem A into problem B, and you are done. Reduction can be applied recursively: If problem A can be solved through problem B, and problem B can be solved through problem C, then problem A can be solved through problem C in two steps. Hence, we end up with a complex stack of software machines: Python runs as an interpreter on an operating system that runs on a hypervisor that runs on a processor which is implemented with a microarchitecture. We don’t build a hardware machine to do matrix multiplication; instead, we write a Python program and call it a day. But that shortcut appears to cost tremendously in efficiency.

Better Algorithms

In addition to better software, Dr. Leiserson observes that better algorithms are needed. Algorithms are invented (like science) rather than evolved (like engineering). Hence, a new insight into how to solve, for example, graph optimization, can suddenly decrease the complexity order of the problem and cause a jump in performance of 10x or more.

Better algorithms require careful design and development. Progress in algorithm design has relied on three kinds of advancements:

  1. Attacking new problem domains: Novel problems such as machine learning, post-quantum cryptography, social networking, and robotics have spurred innovation in problem-solving.

  2. The need for scalability: This has pushed algorithm designers toward finding better solutions that can handle larger data sets. For example, estimating the average of a large data set by computing the average of a random sample of the data set is a means to quickly estimate the average. Similarly, approximate computing has developed techniques to derive answers that are close to correct, often with large gains in performance and resource cost.

  3. Tailoring algorithms toward the hardware: Historically, algorithms have been developed against a single-thread random-access machine. New algorithms, however, may take into account the multi-core structure of GPUs or the distributed nature of FPGA fabric. Developing an algorithm with the final architecture in mind is one way to bring algorithms closer to hardware, but it is not easy.

Better Hardware Architecture

The third area of improvement enumerated in Dr. Leiserson’s paper is hardware architecture. In the past, the role of hardware was straightforward: transistor sizes shrink with every generation, so using more transistors to solve a given problem is an easy way to handle performance improvement by technology.

Clock frequency increases are no longer a source of improvement, either. Since 2006, the so-called Dennard scaling has ended. Dennard observed that the smaller feature sizes of every hardware generation allow for a reduction in voltage (to keep the electric field constant in a smaller transistor) and an increase in clock speed (because of a smaller, faster transistor). The net effect of Dennard scaling was that the power per transistor remained more or less constant, as the voltage went down and the frequency went up. However, because transistor density increased, power density increased as well. Around 2006, the limit of power density that can be tolerated on-chip was reached, meaning that future generations of chips still use lower voltages, but not higher clock frequencies.

So in the future, every transistor will have to become more efficient because you will not automatically get more transistors with every new technology generation. In other words, for a given functionality X, you will need to be able to accomplish that functionality with fewer (not more!) transistors because that is the only way to increase hardware parallelism on-chip.

A good example of this observation is the SPECINT benchmark, a benchmark to measure the efficiency of a processor. Since 2004, single-core machines have demonstrated a 3x performance gain, while multicore machines have demonstrated a 20-30x performance gain.

Innovation in hardware architecture must come from two factors:

  1. Use simple processors, but use lots of them per chip. This increases the overall parallellism on chip.

  2. Use domain specialization and apply hardware specialized towards a single task. Example success stories include the GPU or Google’s Tensor Processing Unit (TPU).

An excellent historical study of computer architecture and the crucial role of hardware is offered by Hennessy and Patterson’s review paper. They review several seminal architectures and highlight their role in computer history. Hennessye and Patterson concludes that there are three major opportunities for future computer architecture improvements.

  1. Better programming of cores. Note that this is similar to Leiserson’s argument who says that software and hardware should live closer together.

  2. Domain specific architectures such as GPU, network processors, deep learning processors, software-defined radios, will offer the next level of improvements in programmable machines. Domain-specific architectures, or DSA for short, outperform classic general-purpose machines for three reasons. First, they offer better parallellism. Second, they provide better memory hiearchies for the problem at hand. Third, the allow for custom precision in their operations. Examples of successful DSA’s today are GPU’s and TPU’s.

  3. Open architectures (think RISC-V) will enable a broader range of innovation opportunities by enabling customization at every level of processing abstraction.

The technological limits are defined by power and interconnections

Leiserson’s paper does not describe the physical limitations that prevent us from building faster and faster computers. A few years ago, Markov tried to capture these limitations in an article on Limits on Fundamental Limits to Computations. He concludes, though, that the constraints that will end Moore’s law are not limited to a single technological domain but multiple ones, including manufacturing, energy, physical space, design, and algorithms.

Markov highlights the challenges in further scaling integrated circuits, such as the Abbe diffraction limit in manufacturing, which restricts the minimum feature size in semiconductor fabrication. He also discusses the issues with interconnect scaling and power consumption, noting that these factors have become significant bottlenecks in modern computing.

There is also the challenge of energy-time trade-offs. The end of CPU frequency scaling has led to a shift toward multicore processors and “dark silicon”—where portions of a chip are kept inactive to manage power density. He also touches on fundamental physical limits like Landauer’s principle, which links information processing to thermodynamic costs.

Then there are also limits to parallelism and the complexity-theoretic challenges, particularly in solving NP-hard problems, and the difficulties in achieving substantial speedups through parallel computing. Markov concludes that while many limits in computation are currently being pushed, some are becoming increasingly stringent, presenting significant challenges for future advancements in computin. An observation could be made that the current state of AI almost guarantees a boundless demand for additional compute power – so that the fundamental limit in exploiting parallellism is perhaps not as stringent as other limitations.

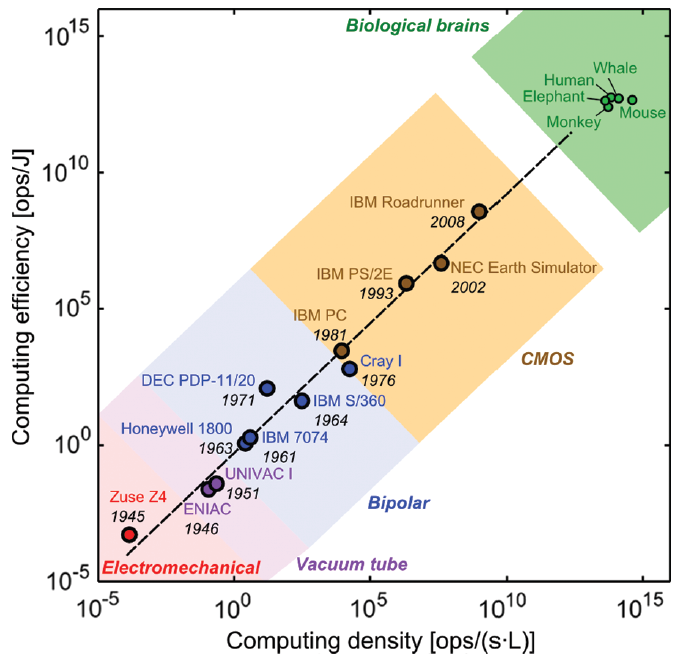
A few years before Markov’s paper, Ruch and colleagues wrote a visionary document that tries to define the scaling problem in VLSI as a five dimensional, rather than a three-dimensional problem. They observe traditional chips are 2D structures, and that current state of the art supports 3D integration. Technologies such as multi-chip modules and stacked die allow us to use a third dimension which drastically increases the density of the computer. Nevertheless, such a 3D computer creates two additional scaling dimensions. First, the increased density of computing generates heat, so cooling becomes an important issue. Second, the increased density of computing creates a significant interconnection challenge, as these ultra-dense computers need an ever increasing amount of inteconnections. Nevertheless, the authors advocate the use of 3D chip stacks with combined electrochemical power delivery. Furthermore, they show that the a higher compute density leads to better energy efficiency. At the apex of efficiency and compute density sits, perhaps not suprisingly, the biological brain, which remains several orders of magnitude more dense and more energy efficient than the best computer we can build today.

_images/ibmdensity.png