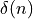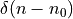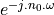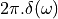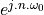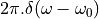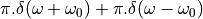Signal Sampling and Reconstruction
Important
The purpose of this lecture is as follows.
To review the essentials of signal sampling (Dirac Impulse, DTFT)
To review the lab kit’s internal hardware and software that controls sampling
Perfect Sampling using the Dirac Impulse
In the first half of this lecture, we will talk about ‘ideal’ sampling and discuss the standard representation of ideal sampling.
The Dirac Impulse
We will recap some of the basic properties of the
spectra of discrete-time signals. Consider the basic Dirac pulse 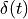 at time
at time 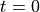 . The spectrum of this pulse is given by the Fourier Transform:
. The spectrum of this pulse is given by the Fourier Transform:
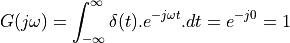
The spectrum of an impulse contains every frequency under the sun. Furthermore,
the magnitude and the phase of 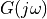 have a particular format.
have a particular format.
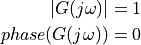
The amplitude of every phasor making up 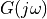 is uniform, and
they are all aligned with each other (at t=0). It is this alignment that
causes such a sharp impulse to appear in the time domain.
is uniform, and
they are all aligned with each other (at t=0). It is this alignment that
causes such a sharp impulse to appear in the time domain.
At any time besides t=0, the combination of frequencies in 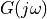 will cancel each other out, so that the time-domain value
of
will cancel each other out, so that the time-domain value
of 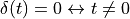 .
.
To see why, consider the behavior of the spectrum, as in the following
picture. Since 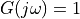 , each frequency contains a phasor of
unit length. As time progresses, all of these phasors start to rotate at the
speed corresponding to its frequency. When
, each frequency contains a phasor of
unit length. As time progresses, all of these phasors start to rotate at the
speed corresponding to its frequency. When 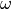 is positive, they
rotate counter-clockwise. When
is positive, they
rotate counter-clockwise. When 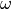 is negative, they rotate
clockwise.
is negative, they rotate
clockwise.
The reponse of the function in the time domain is the sum of all these
phasors. At time zero, all phasors (at every frequency) are aligned with the
real axis, and pointing upward. This makes 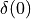 an infinitely
high and infinitely narrow pulse with area 1. If time advances one second,
the phasors will rotate. After one second, the phasor at
an infinitely
high and infinitely narrow pulse with area 1. If time advances one second,
the phasors will rotate. After one second, the phasor at 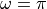 has made a half turn, while the phasor at
has made a half turn, while the phasor at 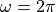 has made a
full turn. The time domain response at time = 1 will be zero, since as the
sum of all phasors (over all
has made a
full turn. The time domain response at time = 1 will be zero, since as the
sum of all phasors (over all 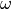 ) cancels out to 0. This is true
for every
) cancels out to 0. This is true
for every 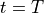 , since it is always possible to find a
frequency
, since it is always possible to find a
frequency 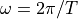 that has made a full turn at that
moment, thereby cancelling out the response of frequencies between DC
and
that has made a full turn at that
moment, thereby cancelling out the response of frequencies between DC
and 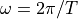 .
.

The time-shifted Dirac Impulse
Next, consider the spectrum of a Dirac pulse at a time different from zero,
say 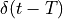 for a Dirac pulse at time
for a Dirac pulse at time 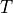 . Clearly, this
pulse must also contain the same frequency components as
. Clearly, this
pulse must also contain the same frequency components as 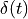 . The only difference is that
. The only difference is that 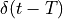 has shifted over
time
has shifted over
time 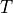 , which will induce a delay for all of these frequency
components. The spectrum is now given by:
, which will induce a delay for all of these frequency
components. The spectrum is now given by:
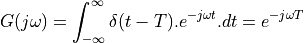
The term 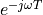 still has unit magnitude for all frequencies,
but there is a phase shift of
still has unit magnitude for all frequencies,
but there is a phase shift of 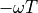 radians for the phasor at
frequency
radians for the phasor at
frequency 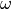 .
.
The makes the term 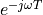 pretty important. This term
describes the spectrum of a pulse delayed by time T. When we think of a
sampled-data signal as a sequence of weighted pulses, we can thus construct
the spectrum of the sampled-data signal by summing up the contribution of
each pulse individually. Since the complete sampled data signal is a linear
combination of weighted time-delayed pulses, the spectrum of a sampled data
signal is a linear combination of the spectrum of these individual pulses.
pretty important. This term
describes the spectrum of a pulse delayed by time T. When we think of a
sampled-data signal as a sequence of weighted pulses, we can thus construct
the spectrum of the sampled-data signal by summing up the contribution of
each pulse individually. Since the complete sampled data signal is a linear
combination of weighted time-delayed pulses, the spectrum of a sampled data
signal is a linear combination of the spectrum of these individual pulses.
Indeed, let’s say that you have a sampled-data signal 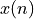 . Then the
signal can be written in the time domain as
. Then the
signal can be written in the time domain as 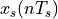 as follows:
as follows:
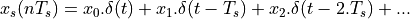
Now, making use of the linear property in frequency analysis, we can express
the spectrum of 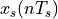 as the sum of the spectra caused by each
single sample pulse. Mathematically:
as the sum of the spectra caused by each
single sample pulse. Mathematically:
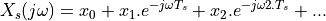
This is quite cool: you can describe the frequency spectrum of a sampled-data
signal simply by looking at the sampled-data values! This transformation also
demonstrates that the spectrum of a sampled-data signal is periodic,
since 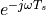 is periodic. In particular, the period
is
is periodic. In particular, the period
is 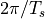 . Indeed, recall from Lecture 1 that the spectrum of a
sampled data signal contains infinitely many copies of the spectrum of the
baseband signal. When the baseband signal has no components below
frequency
. Indeed, recall from Lecture 1 that the spectrum of a
sampled data signal contains infinitely many copies of the spectrum of the
baseband signal. When the baseband signal has no components below
frequency 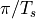 , then the baseband signal can be perfectly
recreated from the sampled-data signal.
, then the baseband signal can be perfectly
recreated from the sampled-data signal.
The Discrete Time Fourier Transform
The previous expression is very close in form to the Discrete Time Fourier Transform.
Important
The Discrete Fourier Transform is the spectrum of a sample-data
signal 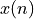 given a normalized sample period of
given a normalized sample period of 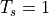 .
.
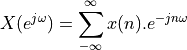
Here are some well-known DTFT pairs.
Sequence |
Discrete-Time Fourier Transform |
|---|---|
|
1 |
|
|
1 |
|
|
|
|
|
The last formula, for 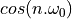 , is somewhat particular, since
for many sample sequences
, is somewhat particular, since
for many sample sequences 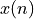 it’s not easy to find a closed form.
That brings us to the z-Transform.
it’s not easy to find a closed form.
That brings us to the z-Transform.
The z-Transform
The z-transform is a generalization of the DTFT where we write a sampled-data
sequence as a power series in  , where
, where 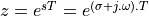 has both real and imaginary components.
has both real and imaginary components.
The z-transform of a sampled-data signal becomes:
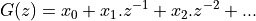
When  equals the imaginary term
equals the imaginary term 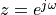 , then
, then 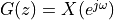 as in the DTFT. However, in
contrast to the DTFT, the z-transform is better at handling long
series
as in the DTFT. However, in
contrast to the DTFT, the z-transform is better at handling long
series 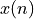 where summing up
where summing up 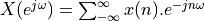 is complicated.
is complicated.
Here is an example. Suppose we have a unit step:
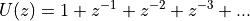
Which is tricky to sum up using 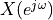 , since the sum does not
converge for
, since the sum does not
converge for 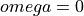 . In the z-transform expression, we can
rewrite
. In the z-transform expression, we can
rewrite 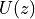 as a power series. Namely
as a power series. Namely
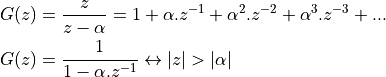
Hence, the z-transform of the unit step can be written as
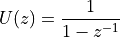
The choice of  is inspired by the Laplace transform variable s. But
unlike the Laplace transform, the
is inspired by the Laplace transform variable s. But
unlike the Laplace transform, the  has built-in periodicity
has built-in periodicity 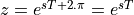 .
.
The Unit Circle
z-transform functions are commonly represented (and computed) on a unit circle
presentation, which reflects the periodic nature of  . In fact, the
z-plane (which contains the unit circle) is the discrete-time equivalent of
the s-plane for continuous-time functions. The inside of the unit circle
corresponds to the left side of the s-plane (stable side) while the outside
of the unit circle corresponds to the right side of the s-plane. The unit
circle itself maps to the frequency axis in the s-plane, and any feature in
the z-plane at an angle
. In fact, the
z-plane (which contains the unit circle) is the discrete-time equivalent of
the s-plane for continuous-time functions. The inside of the unit circle
corresponds to the left side of the s-plane (stable side) while the outside
of the unit circle corresponds to the right side of the s-plane. The unit
circle itself maps to the frequency axis in the s-plane, and any feature in
the z-plane at an angle 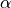 will repeat forever in the s-plane
at
will repeat forever in the s-plane
at 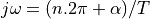 .
.

Signal Sampling on the MSP432
The MSP432 on the lab kit contains a 14-bit successive-approximation ADC. The
ADC is fully configurable from software. In the following, we summarize the
operation of the ADC as used by the XLAUDIO_LIB. Detailed information
on the MSP432 ADC can be found in the MSP432 Technical Reference
Manual.
First, let’s summarize the design abstraction levels that are relevant to understand the operation of sampling from a technical perspective. From the lowest abstraction level (i.e., closest to hardware) to the highest abstraction level(i.e., closest to the software application), we enumerate the abstraction levels as follows.
Hardware Schematics: The physical implementation of the MSPEXP432P401R board and the audio frontend BOOSTXL_AUDIO are each described in a user manual, the
MSPEXP432P401R User Guideand theAUDIO-BOOSTXL User Guide. These user guides show the physical connections of components on the board, including the connector pin definitions as well as the schematics.Hardware Details: Additional documentation on the hardware details of individual components on these PCB’s is captured in the datasheets for these components. For MSP432 is a fairly complex microcontroller, which has a
datasheetand a low-leveltechnical reference manual. The datasheet lists device-specific information (such as the precise configuration of pin-to-peripheral assignments), while the technical reference manual describes how to program the MSP432 peripherals.Hardware Abstraction Library: The low-level programming on the MSP432 is handled through a separate library (aptly named DriverLib) which is part of the MSP432P401R Software Development Kit. The documentation for this library can be found through CCS Resource Explorer. It can also be
downloaded as a PDF. This library introduces higher level functions that simplify peripheral programming.DSP Application Library: To make the programming of DSP applications on the MSP432 easier, we have added a software layer on top of the DriverLib. This software library, called XLAUDIO_LIB, was developed specifically for this class, and its documentation is available on the course website.
DSP Application: Finally, the application software forms the top of this stack. The application software for real-time DSP projects in this class will be written using a cyclic-executive model, ie. there is no RTOS involved.
Let’s consider these abstraction levels for the case of the loopback application of Lab 1.
Microphone Pre-amp
In the schematics of the AUDIO-BOOSTXL board, we find a schematic the microphone pre-amplifier:

This is a non-inverting op-amp configuration with a gain of approximately 250
(200000 / 820). At the output of the pre-amplifier, there’s a first-order
low-pass filter with a cut-off frequency of 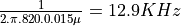 . Such lowpass filters are very common before
analog-to-digital conversion, as they help ensure that the analog input
signal is bandwidth limited.
. Such lowpass filters are very common before
analog-to-digital conversion, as they help ensure that the analog input
signal is bandwidth limited.
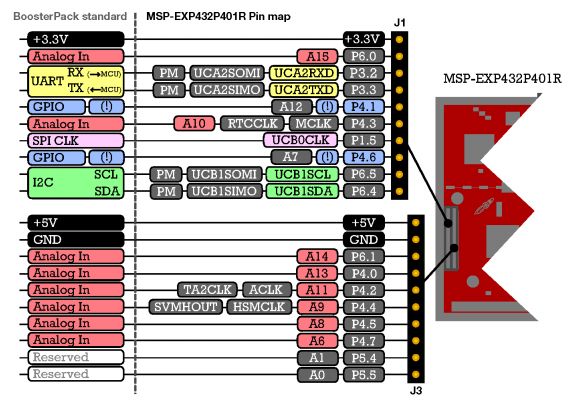
Next, the amplified microphone signal is wired to a header pin of the AUDIO-BOOSTXL board, and from there to a corresponding header pin on the MSP432 board. To find the pin definitions of each of these headers, you have to consult the User Guide for each board. The microphone is wired to the ‘Analog In’ pin of the BoosterPack header, which in turn is connect to a pin labeled A10 RTCLK MCLK P4.3. The important piece of information is A10, which stands for ‘ADC input channel 10’. That input pin is shared with several other microcontroller functionalities (RTCLK MCLK P4.3) - which will be inactive when we use the pin as an analog input pin.

MSP432 Microcontroller
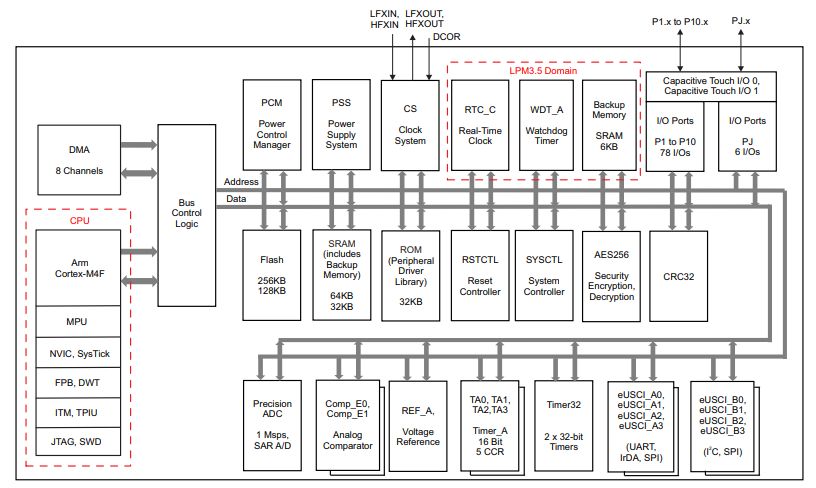
We are now in the MSP432 microcontroller. The MSP432 datasheet gives a summary of the (large) amount of peripherals present in this microcontroller. One of them is the ADC. Signal samples are transported over the internal data bus to an ARM Cortex-M4F processor. The ARM Cortex-M4F is a RISC micro-processor with a three-stage pipeline.
The ‘F’ suffix in ‘Cortex-M4F’ indicates that the micro-processor has a built-in floating point unit. For our DSP experiments, this is an advantage as we can write C code using floating-point numbers. While floating-point accuracy is standard (and expected) on high-end processing platforms such as your laptop, is it considered a prime feature on micro-controllers. We will come back to this aspect in one of the future lectures.
ADC14 Peripheral
Next, we zoom in to the ‘Precision ADC’ block and consider the internal operation. The ADC has in input multiplexer that can select between one out of 23 analog sources. The ADC has a 14-bit resolution and uses a successive approximation architecture. The sample-and-hold operation which we discussed at the start of the lecture, is at the center of the ADC. The ADC conversion is started by asserting SAMPCON. It can be asserted by software (called a ‘software trigger’), are by an external source such as a timer. When the ADC conversion finishes, the module can optionally generate an interrupt.

In the Lab 1 loopback example, the ADC is used as follows. A timer module will trigger a conversion at regular intervals. With the XLAUDIO_LIB, the conversion rate can be selected between 8KHz and 48KHz. When the conversion in the ADC finishes, the ADC calls an end-of-conversion interrupt service routine (ISR). That ISR, in turn, can call a user-defined callback function. Your DSP code is integrated inside of this ISR callback function. Thus, with a conversion rate set at 16KHz, for example, your callback function is called 16,000 times per second, each time with a new converted output x.

The resolution of the ADC is 14 bit. With the input voltage 0V, the output code is 0x0000. With the input voltage 3V3, the output code is 0x3FFF (that is, 14 bits all set to ‘1’). In between, the encoded value increases linearly.
Signal Reconstruction
The conversion of a discrete sequence of numbers 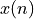 to a continuous-time signal
to a continuous-time signal
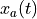 is called signal reconstruction. Because of the Nyquist
is called signal reconstruction. Because of the Nyquist
theorem, we know that
can be perfectly reconstructed by a simple filter operation.

Such a brick-wall filter is called an ideal reconstruction filter. It has an impulse response in the shape of a sinc function.
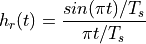
The sinc function interpolates between successive samples. 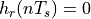 for every value of
for every value of 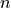 except for 0. The sinc function has a
response for
except for 0. The sinc function has a
response for 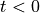 , which means that it is non-causal and therefore
cannot be implemented as is.
, which means that it is non-causal and therefore
cannot be implemented as is.
Here is the response of the filter on a single impulse in a stream of zero-valued samples.

When the sample stream takes on random values, each of these random-valued pulses creates a sinc response, and all of these sinc combine to create an ideal (bandwidth-limited) interpolation of the sequence of random-valued pulses.

Practical Signal Reconstruction
Because the ideal reconstruction filter cannot be implemented, in practice it is approximated. Many Digital-to-Analog converters, including the one used in our AUDIO-BOOSTXL kit, uses a zero-order hold reconstruction. The idea of a zero-order hold is to maintain the signal level of the previous pulse until the next pulse arrives. This leads to a staircase curve:
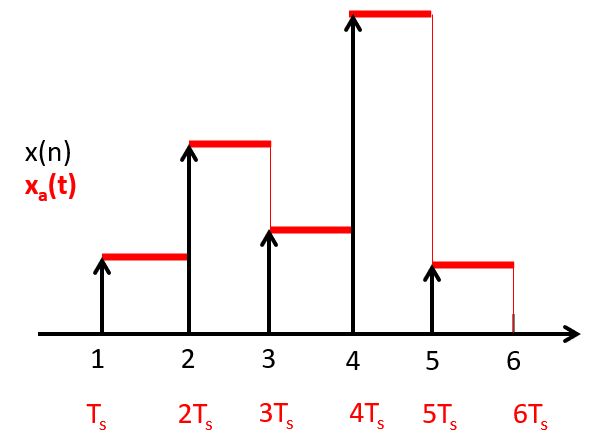
It’s useful to consider the distortion resulting from the zero-order hold
reconstruction. Clearly, the shape of the reconstructed 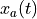 is
quite different from the one which was originally sampled.
is
quite different from the one which was originally sampled.
The zero-order hold reconstruction filter has an impulse reponse  :
:
This reconstruction filter has the following frequency response:
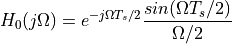
The important property of this frequency response is that it has zeroes at
multiples of the sample frequency, 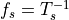 . The effect of the
zero-order hold filter on the frequency response of the sampled-data
signal
. The effect of the
zero-order hold filter on the frequency response of the sampled-data
signal 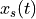 shows the frequency response of the imperfectly
reconstructed
shows the frequency response of the imperfectly
reconstructed 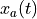 .
.

Signal Reconstruction on the MSP432
The MSP432 does not have an on-board DAC. Instead, there is a 14-bit D/A converter on the AUDIO-XL board. This D/A converter is controller through an SPI interface on the MSP432, in addition to a SYNC pin.

We first discuss the implementation on the AUDIOXL board, and next discuss the
SPI interface between the MSP432 and the AUDIO-XL board. The DAC is driven
through a serial SPI interface. The DAC has a zero-order hold response, and
this response can be observed by connecting an oscilloscope probe to pin 2 or
pin 4 of connector J5. However, the signal that is driving the audio
amplifier is passed through a lowpass filter with a cutoff frequency of
approximately 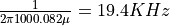 . This means
that the sincx effect of the staircase reconstruction may roll off quicker at
higher frequencies. However, when you generate signals with a sample
frequency below 20KHz, you should be able to observe parts of the
sampled-data spectrum
. This means
that the sincx effect of the staircase reconstruction may roll off quicker at
higher frequencies. However, when you generate signals with a sample
frequency below 20KHz, you should be able to observe parts of the
sampled-data spectrum  beyond the Nyquist frequency.
beyond the Nyquist frequency.
Note
In high-end audio systems, a signal construction filter would be much more sophisticated; it would eliminate any frequency beyond the Nyquist frequency, and it would eliminate the amplitude distortion caused by zero-order hold below the Nyquist frequency. The simplicity of the signal reconstruction hardware on our lab kit allows you to investigate the consequences of ‘imperfect’ signal reconstruction.
DAC8311 Chip
Next, we discuss the communication between the MSP432 and the DAC chip. The SPI interface communicates one byte at a time, so 14 bits for the DAC are transferred using a high byte and a low byte. The DAC has a SYNC pin which is asserted to indicate when the first byte is transmitted. The bits are transmitted MSB to LSB, and the DAC datasheet (DAC8311) illustrates the timing.
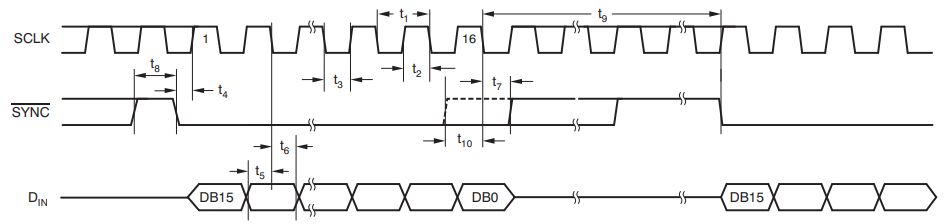
The MSP432_BOOSTXL library includes a software function,
DAC8311_updateDacOut(uint16_t value), which writes a new value to the
DAC:
1void DAC8311_updateDacOut(uint16_t value) {
2 // Set DB15 and DB14 to be 0 for normal mode
3 value &= ~(0xC000);
4
5 DAC8311_writeRegister(value);
6}
7
8static void DAC8311_writeRegister(uint16_t data) {
9 // Falling edge on SYNC to trigger DAC
10 GPIO_setOutputLowOnPin(DAC8311_SYNC_PORT,
11 DAC8311_SYNC_PIN);
12
13 while (EUSCI_B_SPI_isBusy(DAC8311_EUSCI_BASE)) ;
14 EUSCI_B_SPI_transmitData(DAC8311_EUSCI_BASE, data >> 8); // high byte
15
16 while (EUSCI_B_SPI_isBusy(DAC8311_EUSCI_BASE)) ;
17 EUSCI_B_SPI_transmitData(DAC8311_EUSCI_BASE, data); // low byte
18
19 while (EUSCI_B_SPI_isBusy(DAC8311_EUSCI_BASE)) ;
20
21 // Set SYNC back high
22 GPIO_setOutputHighOnPin(DAC8311_SYNC_PORT,
23 DAC8311_SYNC_PIN);
24}
Distortion in the Sampling and Reconstruction Process
Finally, we summarize the sources of distortion in the sampling and reconstruction process. We can now understand the causes and effect of each type of distortion.
1. Aliasing is caused when a continuous-time signal is sampled at a rate below twice the highest frequency component in that continuous-time signal. Aliasing causes overlap between adjacent frequency bands in the discrete-time signal, and it causes non-recoverable distortion.
2. Quantization Noise is caused because the disrete-time signal is quantized on a finite number of quantization steps. Quantization noise is a non-linear effect, and its effect is often modeled as additive noise. We will investigate quantization noise in more detail when we discuss filters.
3. Jitter is caused by imperfect sampling, and is visible by random shifts back and forth in time. Jitter is a non-linear effect as well, and eventually appears as noise in the reconstructed signal.
4. Zero-order Hold is an effect in the signal reconstruction process where imperfect reconstruction is used instead of ideal sinc interpolation. A zero-order hold is a linear (filter) effect, which can be compensated by proper reconstruction filter design.