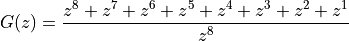FIR Implementation Techniques ¶

Contents

FIR Implementation Techniques

Important

The purpose of this lecture is as follows.

To review the essentials of signal sampling (Dirac Impulse, DTFT)
To review the lab kit’s internal hardware and software that controls sampling

Direct-form and Transpose-form FIR implementation ¶

The Z-transform of an FIR is a polynomial in 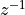$z^{-1}$ .

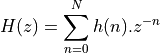
$H(z) = \sum_{n=0}^{N} h(n) . z^{-n}$

The sequence 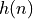$h(n)$ is the impulse response of the FIR filter. This sequence is bounded.

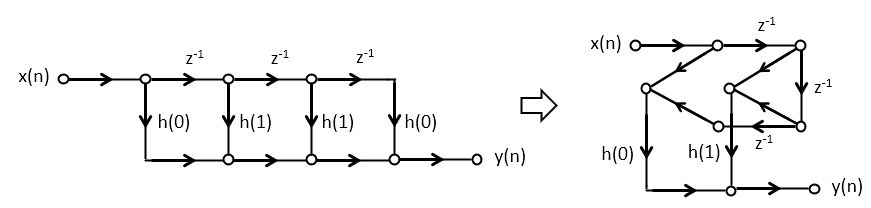
The classic direct-form implementation of an FIR filter is done by implementing a tapped delay line. The following is an example of a third-order FIR filter. Such a filter would have three zeroes in the z-plane and three poles at 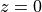$z=0$ . It has 4 multiplications with coefficients, 3 additions, and three delays.

Interestingly, the impulse response of the FIR can be produced by an alternate structure, called the transpose-form implementation. Unlike the direct-form implementation, the transpose-form implementation multiplies an input sample with all filter coefficients at the same time, and then accumulates the result. Note that the order of the impulse response coefficients is reversed.

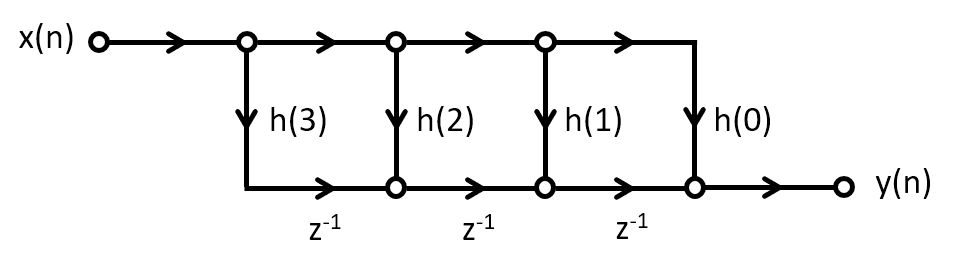
Optimizing for Symmetry (Linear Phase FIR)¶

We already know that the time-domain shape of a signal is determined by both the phase information as well as the amplitude information of its frequency components. If phases are randomly changed, then the time-domain shape will be distored.

For example, instead of measuring the frequency response of a filter using an impulse, we can measure the frequency response as well using noise. Random noise contains all frequencies, just like a Dirac impulse. But unlike a Dirac impulse, random noise has random phase. Therefore, we have a time domain response spread out over time, rather than a single, sharp impulse.

Many applications in communications (digital modulation, software radio, etc) rely on precise time-domain representation of signals; we will discuss such an application in a later lecture of the course. In digital communications applications, filters with a linear phase response are desired, because such filters introduce a uniform delay as a function of frequency. In other words: a signal that fits within the passband of a linear phase filter, will appear undistorted at the output of the filter.

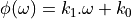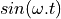Indeed, assume that the phase response is of the form $\phi(\omega) = k_1 . \omega + k_0$ . A sinusoid $sin(\omega.t)$ that is affected by this phase change, becomes:

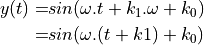
$y(t) =& sin(\omega.t + k_1 . \omega + k_0) \\ =& sin(\omega.(t + k1) + k_0)$

Thus, a linear phase response causes a time-shift of the sinusoid, independent of its frequency. This means that an arbitrarily complex signal, which can be written as a sum of phasors (sines/cosines), will also be affected by a time-shift, independent of its frequency.

Linear phase filters have a symmetric impulse response, and there are four types of symmetry, depending on the odd/even number of taps, and the odd/even symmetry of the impulse response. All of these filters have a linear phase response.

The symmetric response of linear FIR design enables an important optimization for either direct-form or else transpose form FIR designs: we can reduce the number of coefficient multiplications by half. For example, here is an optimized Type-III, 4-tap FIR:

Optimizing Common Subexpressions ¶

The transpose form is convenient when the implementation is able to perform parallel multiplications efficiently, or when parallel multiplications can be jointly optimized.

For example, the following filter coefficient optimization is common in hardware designs of fixed-coefficient FIRs. The transpose form can be optimized for common subexpressions. Since the same input x is multiplied with every filter coefficient at the same time, the common parts of the multiplication can be shared. Consider the impulse response 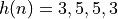$h(n) = {3, 5, 5, 3}$ . This series of coefficients is symmetric, meaning that only a single multiplication with 3 and with 5 is needed. In addition, the multiplications with 3 and with 5 share commonalities. Since 3 = 1 + 2 and 5 = 1 + 4, we can implement these multiplications using constant shifts by 2, and then accumulating the results:

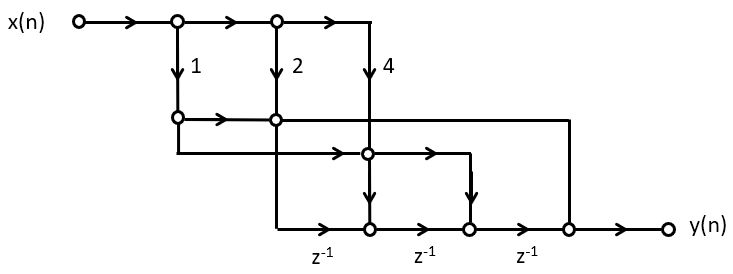
In other words, we can rewrite the following set of expressions:

// input x
// state_variable: d2, d1, d0
// output y
y  = d2 + x * 3;
d2 = d1 + x * 5;
d1 = d0 + x * 5;
d0 =      x * 3;

into the following set of expressions - avoiding multiplications. This would be especially advantageous in a hardware design, because it significantly reduces the implementation cost. In software, where the cost of a ‘*’ operation and a ‘+’ operation are similar, such optimization may have less (or no) impact.

// input x
// temporary variable x2, x4, s3, s5;
// state_variable: d2, d1, d0
// output y
x2 = x  << 1;
x4 = x2 << 1;
s3 = x  +  x2;
s5 = x  +  x4;
y  = d2 +  s3;
d2 = d1 +  s5;
d1 = d0 +  s5;
d0 =       s3;

Cascade-form FIR implementation ¶

A polynomial expression in H(z) can be factored into sub-expressions of first-order factors as follows.

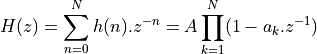
$H(z) = \sum_{n=0}^{N} h(n) . z^{-n} = A \prod_{k=1}^{N}(1 - a_k.z^{-1})$

In the decomposed form, the first-order terms represent the zeroes for H(z). If h(n) is real, then the roots of H(z) will come in complex conjugate pairs, which can be combined into second-order expressions with real coefficients. Such real coefficients are preferable, of course, because they can be directly implemented using a single multiply operation. In addition to providing a more regular design, the cascade implementation also offers better control over the precision and range of intermediate variables. This last point will be discussed later, when we study fixed-point precision implementation aspects.

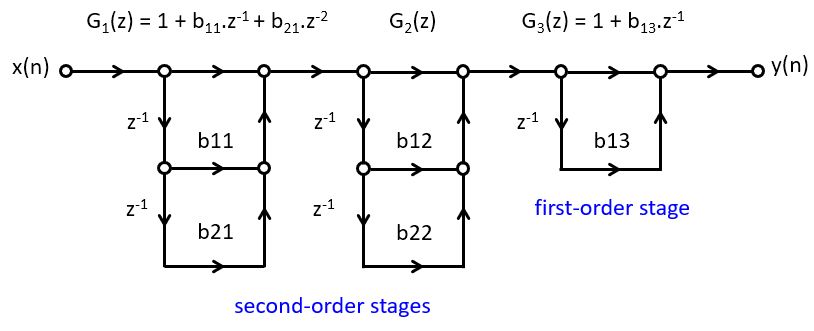
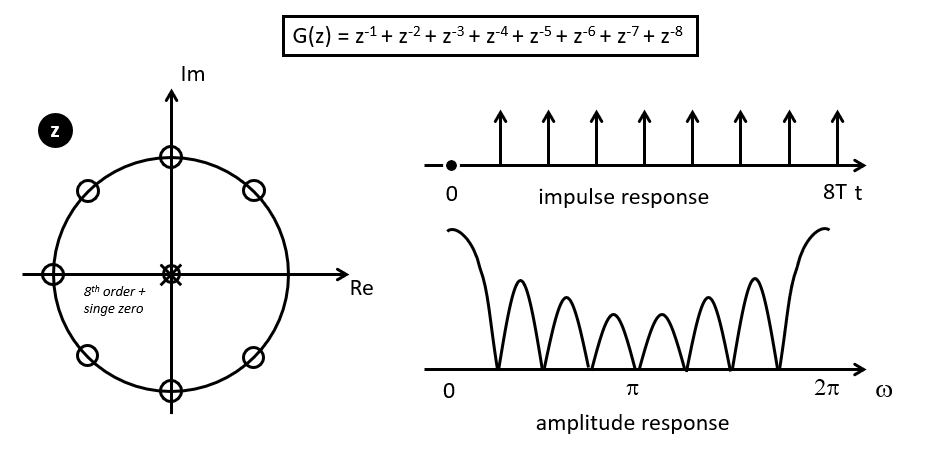
Example - Cascade Design for an averaging filter ¶

Consider the following filter design, which represents an avaraging filter.

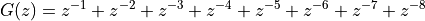
$G(z) = z^{-1} + z^{-2} + z^{-3} + z^{-4} + z^{-5} + z^{-6} + z^{-7} + z^{-8}$

Thus, the filter repeats on input pulse 8 times, starting with one sample delay. This has an averaging effect. To find the zeroes and poles of this filter, note that this FIR can be written as

$G(z) = \frac{z^{8} + z^{7} + z^{6} + z^{5} + z^{4} + z^{3} + z^{2} + z^{1}}{z^8}$

And then you can use a root finding program to find the poles and zeroes of these polynomials. In Matlab, for example, you can use root([0 1 1 1 1 1 1 1 1]) to find the location of these zeroes. Interestingly the zero locations are the same as for the impulse response 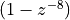$(1 - z^{-8})$ , except for the zero at $z = 1$ .

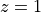C code for the Direct-form Averager ¶

Note

This example is available in the fir_designs repository as fir_averager.

A straightforward implementation of the filter is demonstrated using the following C program.

uint16_t processSample(uint16_t x) {
    static float32_t taps[9];

    // test signal
    // float32_t input = adc14_to_f32(x);

    uint32_t i;
    for (i=0; i<8; i++)
        taps[8-i] = taps[7-i];
    taps[0] = input;

    // the filter. We're adding a scale factor to avoid overflow.
    float32_t r = 0.125f * (taps[1] + taps[2] + taps[3] + taps[4] +
                            taps[5] + taps[6] + taps[7] + taps[8]);

    return f32_to_dac14(r);

    return x;
}

C code for the Averager Cascade Design ¶

Note

This example is available in the fir_designs repository as fir_cascade.

A cascade design works by implementing the FIR filter as second-order sections. These second-order sections are created from the pole-zero plot, by combining complex conjugate zero pairs.

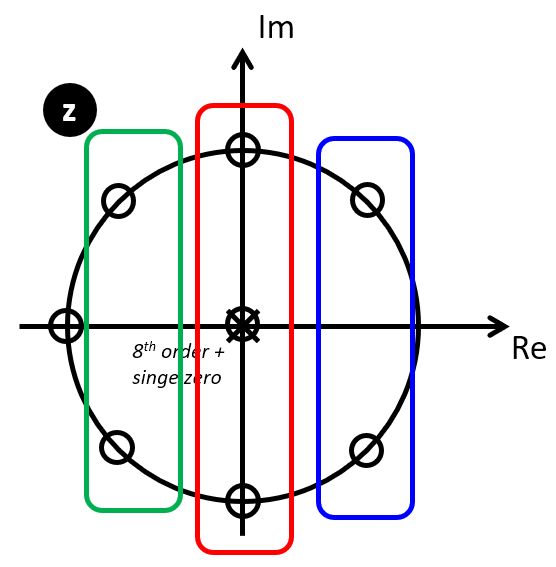
We can identify three complex conjugate zero pairs, which can be written as second-order sections. If a complex conjugate pair has zeroes at locations 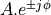$A.e^{\pm j \phi}$ , then the second-order location can be written as follows.

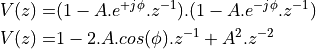
$V(z) =& (1 - A.e^{+ j \phi}.z^{-1}) . (1 - A.e^{- j \phi}.z^{-1}) \\ V(z) =& 1 - 2.A.cos(\phi).z^{-1} + A^2.z^{-2}$

The complex conjugate pairs are located at 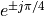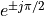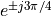$e^{\pm j \pi /4}$ , $e^{\pm j \pi /2}$ , $e^{\pm j 3 \pi /4}$ , which leads to the following second order stages:

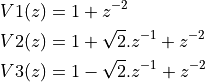
$V1(z) &= 1 + z^{-2} \\ V2(z) &= 1 + \sqrt{2}.z^{-1} + z^{-2} \\ V3(z) &= 1 - \sqrt{2}.z^{-1} + z^{-2}$

Putting everything together, we then obtain the following cascade filter. Note that this design has added an extra delay at the input, as well as an extra zero (at $z=-1$ ).

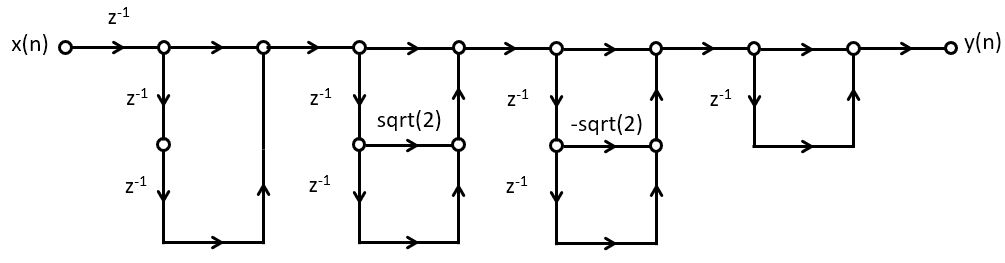
We will now implement this filter in C code. Since the cascade form is repetitive, it makes sense to implement it as a separate function. It’s worthwhile to consider the regularity of this problem. The filter, in essence, can be captured in four cascade filters. Therefore, we will write C code for a single cascade filter, and replicate it in order to create the overall filter.

Let’s start with the single cascade stage. The casecadestate_t is a data type that stores the cascade filter taps as well as the coefficients. Since we are creating a repetition of filters, we have to keep the state as well as the coefficients of the individual stages separate, and this record helps us do that. Next, the cascadefir computes the response on a single casecade stage. The function evaluates the output, and updates the state as the result of entering a fresh sample x. Finally, the createcascade function is a helper function to initialize the coefficients in a casecadestate_t type.

typedef struct cascadestate {
    float32_t s[2];  // filter state
    float32_t c[2];  // filter coefficients
} cascadestate_t;

float32_t cascadefir(float32_t x, cascadestate_t *p) {
    float32_t r = x + (p->s[0] * p->c[0]) +  (p->s[1] * p->c[1]);
    p->s[1] = p->s[0];
    p->s[0] = x;
    return r;
}

void createcascade(float32_t c0,
                   float32_t c1,
                   cascadestate_t *p) {
    p->c[0] = c0;
    p->c[1] = c1;
    p->s[0] = p->s[1] = 0.0f;
}

We are now ready to build the overall filter. This will break down into two functions, the first one to initialize the individual cascade states according to the filter specifications, and the second one to execute the processing of a single sample. The four cascade filters are created as global variables, so that they are easy to access from withing the ADC interrupt callback. The initcascade function defines the coefficients as defined earlier. The M_SQRT2 macro is a pre-defined macro in the C math library that holds the square root of 2. The processCascade function computes the output of the input. The overall filter includes an extra delay (to implement 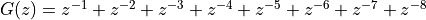$G(z) = z^{-1} + z^{-2} + z^{-3} + z^{-4} + z^{-5} + z^{-6} + z^{-7} + z^{-8}$ ), which is captured with the local static variable d.

cascadestate_t stage1;
cascadestate_t stage2;
cascadestate_t stage3;
cascadestate_t stage4;

void initcascade() {
    createcascade(    0.0f,  1.0f, &stage1);
    createcascade( M_SQRT2,  1.0f, &stage2);
    createcascade(-M_SQRT2,  1.0f, &stage3);
    createcascade(    1.0f,  0.0f, &stage4);
}

uint16_t processCascade(uint16_t x) {

    float32_t input = adc14_to_f32(0x1800 + rand() % 0x1000);
    float32_t v;
    static float32_t d;

    v = cascadefir(d, &stage1);
    v = cascadefir(v, &stage2);
    v = cascadefir(v, &stage3);
    v = cascadefir(v, &stage4);
    d = input;

    return f32_to_dac14(v*0.125);
}

If we run the function and compute the output, we can find that this design has an identical response as the previous direct-form design.

The appeal of the cascade form FIR is the regularity of the design, as well as (as discussed later), a better control over the precision and range of intermediate variables.

Memory Management in FIR ¶

FIR designs can become relatively complex, up to a few hundred taps with coefficients. Hence, at some point the implementation of the FIR delay line becomes an important factor in the filter performance.

Note

This example is available in the fir_designs repository as fir_longfilter.

In a straightforward design, the filter taps are shifted every sample. For an N-tap filter, this means N memory reads and N memory writes. Furthermore, for each memory access, the memory address for the tap has to be computed.

uint16_t processSampleDirectFull(uint16_t x) {
    float32_t input = adc14_to_f32(x);

    taps[0] = input;

    float32_t q = 0.0;
    uint16_t i;
    for (i = 0; i<NUMTAPS; i++)
        q += taps[i] * B[i];

    for (i = NUMTAPS-1; i>0; i--)
        taps[i] = taps[i-1];

    return f32_to_dac14(q);
}

Optimization ¶

A common optimization of delay lines is the use of a circular buffer. To see how to use a circular buffer on a FIR, let’s first consider the memory-access operations for a regular FIR. Each sample period, a new sample enters the filter state. The filter state is then multiplied with the coefficients to compute the filter output, and finally, the filter state is shifted in order to accept the next sample. New samples are entered at a fixed location in the filter state.

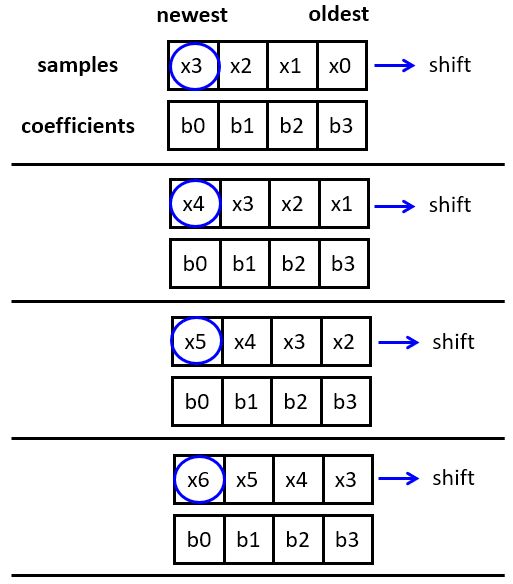
In a circular buffer strategy, we avoid shifting the filter state, but rather change the position where new samples are inserted. New samples will overwrite the oldest sample in the filter state, so that each sample period, the ‘head’ of the filter shifts backward in the array. When the beginning of the array is reached, the head jumps to the back. In this configuration, the ‘first’ tap in the filter state is continuously shifting, and therefore the filter coefficients have to be rotated accordingly. However, this rotation operation is easier to implement than shifting: because the coefficients do not change, the rotation operation can be implemented using index operations.

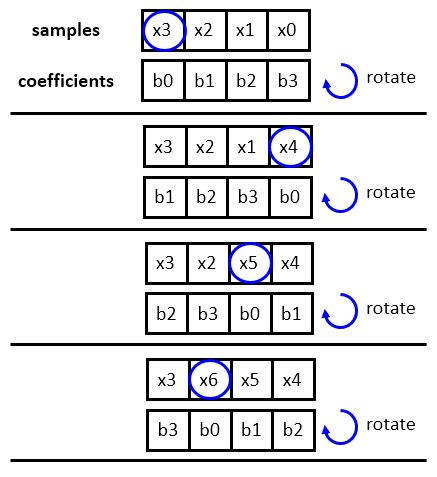
This leads to the following FIR design. Observe that the tap-shift loop has disappeared, while the address expressions have become more complicated. A new head variable is used to indicated the first tap in the filter state. This head circulates to all positions of the delay line until it wraps around.

uint16_t processSampleDirectFullCircular64(uint16_t x) {
    float32_t input = adc14_to_f32(x);

    taps[(64 - head) % 64] = input;

    float32_t q = 0.0;
    uint16_t i;
    for (i = 0; i<64; i++)
        q += taps[i] * B[(i + head) % 64];

    head = (head + 1) % 64;

    return f32_to_dac14(q);
}

Using profiling, we compare the cycle cost of the original FIR design (with shifting) and the optimized FIR design (with a circular buffer). Compiler used: TI v20.2.5.LTS, Full optimization.

FIR Design	16 taps	32 taps	64 taps
tap-shift	379	691	1315
circular buffer	220	373	775
throughput (circular)	1.72x	1.85x	1.69x

Conclusions ¶

We reviewed three different implementation styles for FIR filters: direct-form, transpose-form, and cascade-form filter. The first three are able to implement any filter for which you can specific an finite impulse response. The frequency-sampling filter is a specific design technique that combines filter design and filter implementation.

Next, we also reviewed the impact of memory organization on FIR design. Memory operations are expensive, and the streaming nature of DSP tends to generate lots of memory accesses. FIR designs can be implemented using a circular buffer. The basic idea in memory optimization is to reduce data movement as much as possible, at the expense of more complex memory adderssing.

We have not discussed the design of FIR filters; a tool such as Matlab filterDesigners helps you compute filter coefficients, quantize filter coefficients, and compute amplitude/phase response. Please refer to Lab 2.