Lab 4: Quantization Effects in DSP

The purpose of this assignment is as follows.

to study the impact of quantization on a signal spectrum,
to study the impact of quantization on a filter characteristic,
to measure quantization noise by comparing a floating-point and a fixed-point filter in real time.

Fixed Point Implementation requires Quantization

In class, we discussed a technique to reduce the implementation cost (energy-wise or performance-wise) of a DSP design, by converting the floating-point computations to fixed-point computations. A side-effect of fixed-point design is the requirement to reduce the resolution (precision) of a signal representation. In a fixed-point representation of fix<N,k>, the weight of the least significant bit carries the fixed value 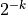$2^{-k}$ , and no changes smaller than that quantity can be represented.

We will study the consequences of the conversion from floating-point representation to fixed-point representation by means of a series of three experiments. For each experiment, you will have to write (or modify) a short program, run it on your board and analyze the resulting signal in the time domain or in the frequency domain. The outcome of this lab consists of the software programs you will write as specified, and the written report with the analysis of the effects you observe.

Impact of Quantization in the time and frequency domain

To support your experiments, you must first write two functions.

int float2q(float x, int f) {
   // .. written by you
}

float2q(x,f) converts a floating point number x to a fixed point number fix<32,f>. The output datatype is an int, a signed integer. The lecture notes explain the relation between floating point representation and fixed point representation.

float q2float(int q, int f) {
   // .. written by you
}

q2float(q,f) converts a fixed point number q of type fix<32,f> to a floating point number.

Add these two functions to program lab4_q1. With these two functions in hand, we can study the effect of fixed-point refinement, that is, we can study the effect of quantization on a DSP program written with float. For example, to quantize the floating point number 0.1 to 5 fractional bits, we write:

float p = q2float(float2q(0.1, 5), 5);

In this example, p will be quantized to 0.09375, which is 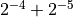$2^{-4} + 2^{-5}$ , or the fractional bitpattern .00011.

Your first task is to analyze the effect of the following signal on the program write a program that passes the input to the output while quantizing the signal to k fractional bits. You can complete the program lab4_q1 to achieve the required implementation for this part.

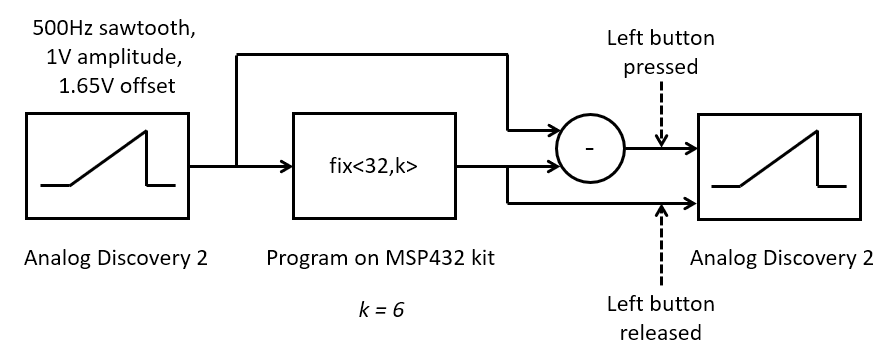
Once you have completed the program, construct the setup as shown on the figure above. Using Analog Discovery 2 Scope, apply a 500Hz sawtooth, 1V Amplitude, 1.65V offset to the ADC input. Observe that this will generate a sawtooth that is centered around 1.65V, so the signal is a sawtooth from 0.65V up 2.65V. Monitor both input and output on the oscilloscope.

Important

Question 1: In the time domain, describe the quantized waveform (left button released) as well as the quantization error (left button pressed). Explain anomalies and non-linearities and pay emphasis to the shape of the signal. You may add a screenshot, or make a drawing, as long as you give a clear understanding of all features you see in the resulting signals.

Impact of Quantization on the Filter Characteristic

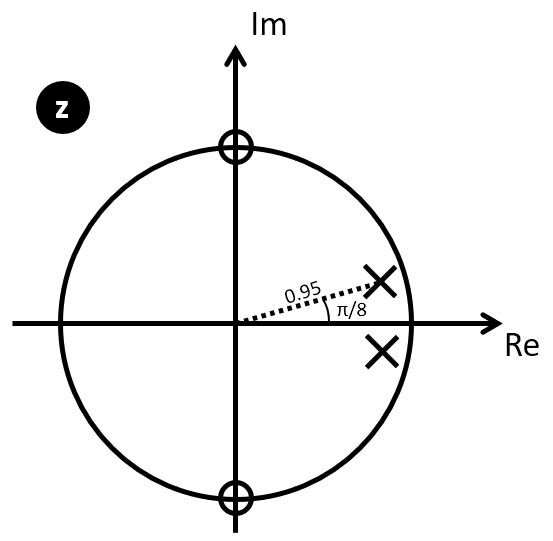
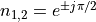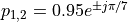Next, we will study the impact of quantization on filter coefficients. You will imlement the following second-order lowpass filter. The zeroes are located at $n_{1,2} = e^{\pm j \pi/2}$ and the poles are located at $p_{1,2} = 0.95 e^{\pm j \pi/7}$ .

Step 1: Floating Point Version in Matlab

Build a reference model for the filter in Matlab, with the same poles and zeroes. Obtain the impulse response of that filter. Don’t use filterDesigner, but use Matlab directly to compute the impulse response. This can be done easily through code as shown below.

b = conv([1 j], [1 -j]);
a = conv([1 -0.95*exp(-j * pi / 7)],[1 -0.95*exp(j * pi/7)]);
x = zeros(100,1);
x(1) = 1.0;

figure(1)
plot(filter(b,a,x)); % plot the impulse response

figure(2)
[h,w] = freqz(b,a); % plot the spectrum and phase
plot(w/pi, 20*log10(abs(h)));

Make a plot of the step response of the filter and keep that aside.

Step 2: Effect of Quantization on Coefficients

Next, you will study the impact of quantization on the filter coefficients. You can do this experiment in Matlab by making use of the fi function, which supports quantization.

Attention

Use help fi in Matlab to learn more about this function.

q = fi(a, 1, 16, 5) creates a quantization version q of the floating point variable a, with a wordlength of 16 bits and 5 fractional bits. To use the quantized variable in computations, use q.data

You can also retrieve the fixed point (integer) representation of the quantized variable with q.dec.

For example, if you quantize the coefficients on 12 fractional bits, then the following program determines frequency response and step response on the quantized coefficients.

b = fi(conv([1 j], [1 -j]), 1, 16, 12);
a = fi(conv([1 -0.95*exp(-j * pi / 7)],[1 -0.95*exp(j * pi/7)]), 1, 16, 12);
x = zeros(100,1);
x(1) = 1.0;

figure(1)
plot(filter(b.data,a.data,x)); % plot the impulse response

figure(2)
[h,w] = freqz(b.data,a.data); % plot the spectrum and phase
plot(w/pi, 20*log10(abs(h)));

Important

Question 2: Write a matlab program that computes the step response and the frequency response of the filter with quantized coefficients for the following quantization factors: 12 fractional bits, 6 fractional bits, and 4 fractional bits.

Explain the impact of quantization. A good strategy is to explain the impact by studying the impact of quantization on the location of poles and zeros of the filter.

Please include a listing of your matlab code, as well as any relevant graphs produced in matlab, in your project report.

Floating-point C Implementation of the Second-order Filter

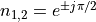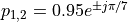Next, you will implement the filter in C and run it on the lab kit. The first version of this filter runs in full floating point, and uses the same specification as defined earlier: the zeroes are located at $n_{1,2} = e^{\pm j \pi/2}$ and the poles are located at $p_{1,2} = 0.95 e^{\pm j \pi/7}$ .

The second-order section filter can be implemented using an architecture of your choice: direct-form I or II, or transposed direct-form. Refer to the examples discussed in class for sample source code for such filters.

Design your filter for an 8 KHz sample rate. The input of the filter is a repetitive impulse with a 1/500 duty cycle (0.2%), which translates to a pulse frequency of 16 Hz. The very low duty cycle is there so you can observe the impulse response of the filter.

Pay attention in choosing the proper triggering settings for the oscilloscope. You have to sample an impulse response that happens 16 times per second, but you have to sample it at a sufficiently high sample rate, say 2 ms/Div on the scope. Thus you may need to add trigger delay in order to capture the signal in its entirety.

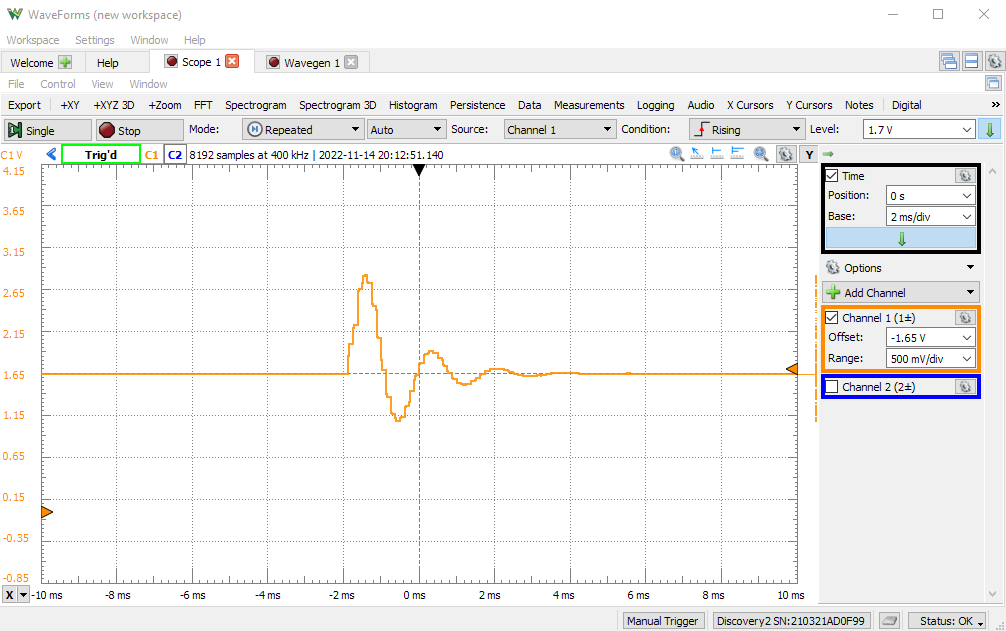
_images/lab4impulsesample.png — Example impulse response. Note that this response was not made for the same coefficient specifications as those above. Your output may look differently.

Important

Question 3: Build the filter and capture its impulse response from the oscilloscope. Compute the spectrum of this impulse response, and compare it to the spectrum computed in Matlab. They should look very similar, of course. Comment on any differences you detect, in the time domain as well as in the frequency domain.

Fixed-point C Implementation of the second-order filter

Once you have a C implementation of the floating-point second-order filter, you can now build the fixed-point equivalent of the filter. Build a flow as in the diagram below: your design needs to include both the floating-point as well as the fixed-point version of the filter.

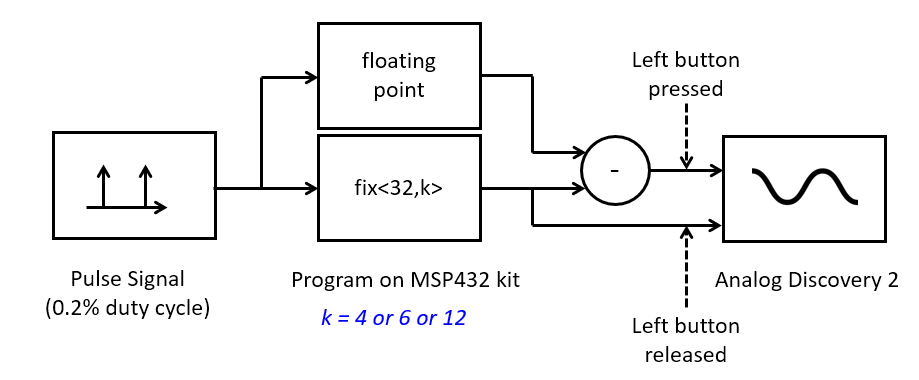
The fixed-point design will have to run a given fractional precision, programmable at 12 bits, 6 bits or 4 bits. Quantization applies to the coefficients; the input signal, the intermediate result, and the output has to be computed using the q15_t datatype (a fixed-point data type with 15 fractional bits).

Your filter needs to support only one quantization level at a time. Thus, your code can use a macro PRECISION which you can set at 12, 6, or 4. You can recompile your code to change the quantization level.

Refer to the example from class for guidance on writing a fixed-point precision filter. In essence, you have to rewrite the solution of Question 3 with fixed-point precision.

Attention

To compare the floating-point and fixed-point version, you may need to use the arm_q15_to_float function which is part of ARM CMSIS DSP, and not the xlaudio library. The project settings have been adjusted to include the following library:

C:\ti\simplelink_msp432p4_sdk_3_40_01_02\source\third_party\CMSIS\DSP_Lib\lib\ccs\m4f\arm_cortexM4lf_math.a

Important

Question 4: Build the filter and capture its impulse response from the oscilloscope for 12, 6 and 4 bits of precision. Compare the impulse response to the impulse response from the floating point design. Comment on any differences you detect in the time domain.

Wrapping Up

The answer to this lab consists of a written report which will be submitted on Canvas by the deadline. Refer to the General Lab Report Guidelines for details on report formatting. You will only submit your written report on Canvas. All code developed must be returned through GitHub.
Follow the four questions outlined above to structure your report. Use figures, screenshots and code examples where appropriate. Please work out the answers in sufficient detail to show your analysis.
Make sure that you add newly developed projects to github: Use the Team - Share pop-up menu and select your repository for this lab. Further, make sure that you commit and push all changes to the github repository on GitHub classroom. Use the Team - Commit pop-up menu and push all changes.
Be aware that each of the laboratory assignments in ECE4703 will require a significant investment in time and preparation if you expect to have a working system by the assignment’s due date. This course is run in “open lab” mode where it is not expected that you will be able to complete the laboratory in the scheduled official lab time. It is in your best interest to plan ahead so that you can use the TA and instructor’s office hours most efficiently.

Good Luck

Grading Rubric

Requirement	Points
Question 1 Analysis	15
Question 2 Analysis	15
Question 3 Analysis	20
Question 4 Analysis	25
All projects build without errors or warnings	5
Code is well structured and commented	5
Git Repository is complete and up to date	5
Overall Report Quality (Format, Outline, Grammar)	10
TOTAL	100