Attention
This document was last updated Aug 22 24 at 21:58
Optimized 32-bit CORDIC Module for GPDK45
Important
The purpose of this lab is as follows.
Study a high-level reference implementation of the CORDIC algorithm in C, including a reference testbench with 1024 test vectors.
Select an optimization strategy (Area or Throughput) and develop an RTL implementation of the CORDIC algorithm, and verify the correctness of the design using the same set of test vectors. Optimizing for area means that your final design must be as small as possible in terms of layout area. Optimizing for throughput means that your final design must compute as many test vectors per second as possible at the maximum clock speed possible with the implemented layout.
Synthesize the design into GPDK45 standard cells. Perform static timing analysis on the design result and demonstrate that your design meets timing.
Create a layout for the design. Perform parastic extraction. Perform static timing analysis on the post-route design and demonstrate that your design meets timing. Perform gate-level simulation using back-annotated post-route timing and demonstrate that your design simulation correctly computes the set of 1024 test vectors.
Summarize your design result in a written report.
Attention
The due date of this lab is 10 November
Introduction
The CORDIC algorithm is an algorithm that efficiently computes transcendental functions (sine, cosine, tangent). CORDIC stands for COordinate Rotation DIgital Computer. The remarkable property of CORDIC is that it requires only integer arithmetic and yet can obtain highly accurate approximutions of sine and cosine functions. There is extensive online documentation of this algorithm, so this lab assigment does not elaborate furter on the algorithm. Some examples references are the following.
Meher, J. Valls, T. -B. Juang, K. Sridharan and K. Maharatna, “50 Years of CORDIC: Algorithms, Architectures, and Applications,” in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 56, no. 9, pp. 1893-1907, Sept. 2009, doi: 10.1109/TCSI.2009.2025803.
Schaumont, P.R. (2010). CORDIC Coprocessor. In: A Practical Introduction to Hardware/Software Codesign. Springer, Boston, MA. doi:10.1007/978-1-4419-6000-9_12
The purpose of this lab is to build an optimized hardware implementation of this algorithm in GPDK45 standard cells. You will go through all steps of Digital Design that we discussed so far: RTL design and optimization, RTL synthesis, static timing analysis, layout, gate-level simulation and gate-level static timing analysis.
Important
In the context of this lab, optimzation means that your design is the best among all submissions. You can optimized for area (layout area as small as possible) or for throughput (final design as fast as possible), so there will be two ‘best’ designs. A portion of your lab grade is directly derived from the rank of your design in the overall ranking in terms of the selected optimization criteria.
You need/may submit only one design, and you may select only one optimization criteria.
Reference Implementation
After you have accepted the assignment, a starter repository will be available for you. Clone it to the design server (your repo name includes your account name).
git clone git@github.com:wpi-ece574-f23/lab-2-patrickschaumont.git
You will obtain the following lab directory structure:
refC |
Reference Implementation in C. Golden model and testvectors |
refV |
Behavioral Implementation in Verilog. Defines the testbench |
rtl |
A Sample RTL implementation of a multiplexed solution |
constraints |
Constraints for the sample RTL implementation |
sim |
Simulation for the sample RTL implementation |
syn |
RTL synthesis for the sample RTL implementation |
sta |
Static timing analysis for the sample RTL implementation |
layout |
Layout for the sample RTL implementation |
glsim |
Gate level simulation for the sample RTL implementation |
glsta |
Gate level STA for the sample RTL implementation |
The golden model is in refC. It contains a CORDIC implementation that computes
sine/cosine of angles in the first quadrant, with a precision of 32 bits and 28
fractional bits (FIX<32,28>). You can compile and run this reference implementation:
cd refC
make
./cordic
Running this program will produce a set of test vectors:
rad c12ac7f cos ba83bca sin af5a193 rad +0.7546 cos +0.7286 sin +0.6850 verif cos +0.7286 sin +0.6850
rad 31102e9 cos fb5011c sin 30c37cf rad +0.1917 cos +0.9817 sin +0.1905 verif cos +0.9817 sin +0.1905
rad bfb8eb2 cos bb80511 sin ae4bea8 rad +0.7489 cos +0.7324 sin +0.6808 verif cos +0.7324 sin +0.6808
In this table, rad represents an encoded input in radians, and cos and sin represent an encoded output. The hex numbers in this output represent FIX<32,28> fixed point numbers. For example, c12ac7f represent a fractional number in radians equal to c12ac7f/(1 << 28) = 0.7546.
This pattern rad, cos, sin is repeated three times. The first is the input/output of the C program in FIX<32,28>. The second group is the input/output of the C program as floating point numbers. The third group is the verification computed using functions of the C math library.
Running this program also creates a test vector file, vectors.txt. The test vector file has three columns: the 32-bit input, and two 32-bit outputs. The output columns can be used to verify the Verilog implementation.
Important
Your design is correct only if it simulates every test vector in vectors.txt correctly. Before proceeding to synthesis/layout, make sure that your RTL design is correct.
Verilog Reference Module
Your design must provide the following I/O ports.
module cordic(
input wire clk,
input wire reset,
input wire start,
input wire signed [31:0] target,
output wire signed [31:0] X,
output wire signed [31:0] Y,
output wire done
);
clk |
I |
positive-edge-triggered clock |
reset |
I |
synchronous active-high reset |
start |
I |
synchronous active-high load signal |
target |
I |
32-bit target input, read when start=1 |
X, Y |
O |
32-bit output with sine and cosine components |
done |
O |
active-high completion signal, mark XY valid |
Verilog Testbench Implementation
The refV directory contains a behavioral (non-synthesizable) Verilog implementation
of the CORDIC module, along with a testbench cordictb.v. This testbench
drives the input/output ports of the CORDIC module with the testvectors
generated under refC. You can reuse this testbench for later testing of the RTL
and gate-level design of your CORDIC.
To simulate, run the testbench as follows.
cd refV
make
You will see the output for each testvector followed by the message ‘TESTBENCH PASSES’. If you don’t see that message, your design is not correct and you have to debug the RTL before continuing.
target 0c12ac7f X 0ba83bca chkX 0ba83bca Y 0af5a193 chkY 0af5a193 OK 1
target 031102e9 X 0fb5011c chkX 0fb5011c Y 030c37cf chkY 030c37cf OK 1
target 0bfb8eb2 X 0bb80511 chkX 0bb80511 Y 0ae4bea8 chkY 0ae4bea8 OK 1
target 00a06e71 X 0ffcdbd8 chkX 0ffcdbd8 Y 00a0625b chkY 00a0625b OK 1
target 1074b5bf X 0841fae1 chkX 0841fae1 Y 0db451be chkY 0db451be OK 1
target 0b414d96 X 0c33af6b chkX 0c33af6b Y 0a597de0 chkY 0a597de0 OK 1
TESTBENCH PASSES
Sample RTL Implementation
To illustrate what steps you have to take during your design, you get one sample solution of an RTL implementation. This design is a multiplexed solution that has not been particularly optimized for area nor throughput. While you may start for your final solution from this design, it’s likely that you may not end up with a good performance rank (since everybody has access to this solution).
To simulate the sample solution:
cd sim
make
To perform RTL synthesis, see below. Note that this is where you select the clock period of your design. The sample RTL implementation is implemented at a clock period of 8ns. Also, note that the RTL synthesis makes use of the constraints SDC file in constraints.
cd syn
make
You can verify that this design meets timing:
cat reports/cordic_report_qor.rpt
Timing
--------
Clock Period
-------------
clk 8000.0
Cost Critical Violating
Group Path Slack TNS Paths
-------------------------------------
clk 1437.1 0.0 0
default No paths 0.0
-------------------------------------
Total 0.0 0
Instance Count
--------------
Leaf Instance Count 1261
Physical Instance count 0
Sequential Instance Count 136
Combinational Instance Count 1125
Hierarchical Instance Count 0
Area
----
Cell Area 2918.628
Physical Cell Area 0.000
Total Cell Area (Cell+Physical) 2918.628
Net Area 0.000
Total Area (Cell+Physical+Net) 2918.628
After synthesis, you also perform static timing analysis:
cd sta
make
In particular, refer to the first path in late.rpt to check the critical path of your design.
cat late.rpt
Path 1: MET Setup Check with Pin Yr_reg[31]/CK
Endpoint: Yr_reg[31]/D (^) checked with leading edge of 'clk'
Beginpoint: A_reg[5]/Q (^) triggered by leading edge of 'clk'
Path Groups: {clk}
Other End Arrival Time 0.000
- Setup 0.119
+ Phase Shift 8.000
= Required Time 7.881
- Arrival Time 6.484
= Slack Time 1.397
Clock Rise Edge 0.000
+ Clock Network Latency (Ideal) 0.000
= Beginpoint Arrival Time 0.000
-----------------------------------------------------------------------------------
Instance Arc Cell Delay Arrival Required
Time Time
-----------------------------------------------------------------------------------
A_reg[5] CK ^ - - 0.000 1.397
A_reg[5] CK ^ -> Q ^ DFFHQX1 0.186 0.186 1.583
gt_88_21_g2159__5477 AN ^ -> Y ^ NAND2BX1 0.082 0.268 1.665
gt_88_21_g2109__2802 A2 ^ -> Y v AOI32X1 0.155 0.423 1.820
gt_88_21_g2098__6417 A1 v -> Y ^ OAI211X1 0.150 0.573 1.970
gt_88_21_g2087__1881 A0 ^ -> Y v OAI211X1 0.167 0.740 2.137
g6174 A1 v -> Y v AO21XL 0.145 0.885 2.282
gt_88_21_g2084__8246 B v -> Y ^ NAND2X1 0.033 0.918 2.315
gt_88_21_g2083__5122 A1 ^ -> Y v AOI21X1 0.102 1.020 2.417
g6168 A v -> Y ^ INVX2 0.164 1.184 2.581
add_90_38_Y_sub_90_49_g2874 A ^ -> Y v INVX2 0.197 1.381 2.778
add_90_38_Y_sub_90_49_g2873__4733 A v -> Y ^ MXI2XL 0.167 1.548 2.945
add_90_38_Y_sub_90_49_g2792__5477 CI ^ -> CO ^ ADDFX1 0.217 1.765 3.162
add_90_38_Y_sub_90_49_g2791__6417 CI ^ -> CO ^ ADDFX1 0.186 1.951 3.348
add_90_38_Y_sub_90_49_g2790__7410 CI ^ -> CO ^ ADDFX1 0.186 2.137 3.534
add_90_38_Y_sub_90_49_g2789__1666 CI ^ -> CO ^ ADDFX1 0.186 2.323 3.720
add_90_38_Y_sub_90_49_g2788__2346 CI ^ -> CO ^ ADDFX1 0.186 2.509 3.906
add_90_38_Y_sub_90_49_g2787__2883 CI ^ -> CO ^ ADDFX1 0.186 2.695 4.092
add_90_38_Y_sub_90_49_g2786__9945 CI ^ -> CO ^ ADDFX1 0.186 2.881 4.278
add_90_38_Y_sub_90_49_g2785__9315 CI ^ -> CO ^ ADDFX1 0.188 3.069 4.466
add_90_38_Y_sub_90_49_g2784__6161 C ^ -> Y v NAND3BXL 0.108 3.177 4.574
add_90_38_Y_sub_90_49_g2783__4733 C0 v -> Y ^ OAI211X1 0.093 3.270 4.667
add_90_38_Y_sub_90_49_g2779__6131 CI ^ -> CO ^ ADDFX1 0.212 3.482 4.879
add_90_38_Y_sub_90_49_g2778__7098 CI ^ -> CO ^ ADDFX1 0.186 3.668 5.065
add_90_38_Y_sub_90_49_g2777__8246 CI ^ -> CO ^ ADDFX1 0.186 3.854 5.251
add_90_38_Y_sub_90_49_g2776__5122 CI ^ -> CO ^ ADDFX1 0.186 4.040 5.437
add_90_38_Y_sub_90_49_g2775__1705 CI ^ -> CO ^ ADDFX1 0.186 4.226 5.623
add_90_38_Y_sub_90_49_g2774__2802 CI ^ -> CO ^ ADDFX1 0.188 4.414 5.811
add_90_38_Y_sub_90_49_g2773__1617 C ^ -> Y v NAND3BXL 0.134 4.548 5.945
add_90_38_Y_sub_90_49_g2769__8428 A1 v -> Y ^ OAI221X1 0.172 4.720 6.117
add_90_38_Y_sub_90_49_g2763__6417 A2 ^ -> Y v AOI31X1 0.171 4.891 6.288
add_90_38_Y_sub_90_49_g2758__9945 A1 v -> Y ^ OAI21X1 0.110 5.001 6.398
add_90_38_Y_sub_90_49_g2755__4733 A1 ^ -> Y v AOI21X1 0.116 5.117 6.514
add_90_38_Y_sub_90_49_g2753__5115 C v -> Y v OR3XL 0.171 5.288 6.685
add_90_38_Y_sub_90_49_g2749__8246 A1 v -> Y ^ OAI221X1 0.093 5.381 6.778
add_90_38_Y_sub_90_49_g2746__2802 CI ^ -> CO ^ ADDFX1 0.219 5.600 6.997
add_90_38_Y_sub_90_49_g2745__1617 CI ^ -> CO ^ ADDFX1 0.186 5.786 7.183
add_90_38_Y_sub_90_49_g2744__3680 CI ^ -> CO ^ ADDFX1 0.186 5.972 7.369
add_90_38_Y_sub_90_49_g2743__6783 CI ^ -> CO ^ ADDFX1 0.184 6.156 7.553
add_90_38_Y_sub_90_49_g2742__5526 B ^ -> Y ^ XNOR2X1 0.163 6.319 7.716
g6091__4733 A1 ^ -> Y ^ AO22XL 0.165 6.484 7.881
Yr_reg[31] D ^ DFFHQX1 0.000 6.484 7.881
-----------------------------------------------------------------------------------
The next step is to generate the layout. Note that the layout makes use of
the chip I/O pin constraints in chip/chip.io. The synthesis step of the layout directly
reads the synthesis netlist produced in syn. Hence, you must complete RTL synthesis
before building the layout.
cd layout
make syn
make layout
When the layout run ends, the script prints the final core area. This is the number that will be used for area cost of your design. This design would measure 6140.61 square micron.
FINAL DESIGN CORE AREA:
@file 173: puts [expr ($xu - $xl)*($yu - $yl)]
6140.61
You can inpect the layout with the gui_show command.
Pay particular attention to white crosses in your design, which indicate design violation errors.
While we did not discuss design violations in detail, a correct design should avoid them. Design
violations can occur because of overly tight design constraints.
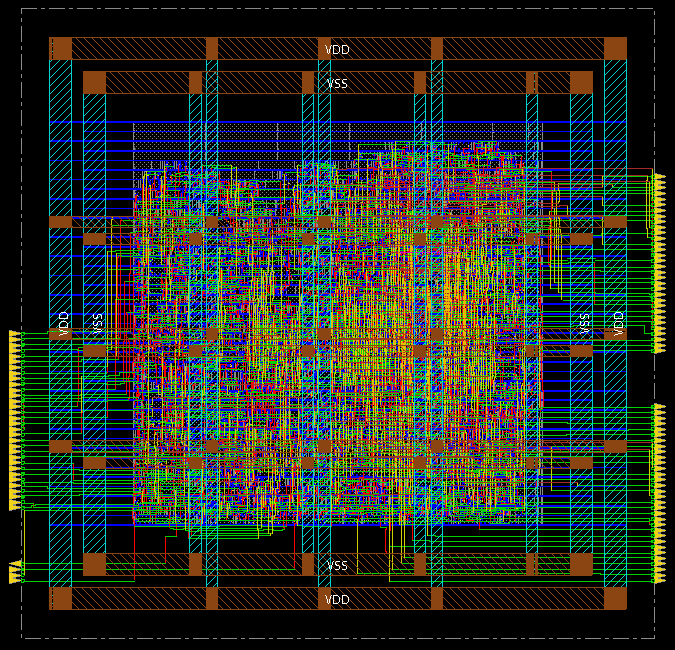
After layout, you can run gate-level simulation
cd glsim
make
The testbench must of course still pass
...
target 00a06e71 X 0ffcdbd8 chkX 0ffcdbd8 Y 00a0625b chkY 00a0625b OK 1
target 1074b5bf X 0841fae1 chkX 0841fae1 Y 0db451be chkY 0db451be OK 1
target 0b414d96 X 0c33af6b chkX 0c33af6b Y 0a597de0 chkY 0a597de0 OK 1
TESTBENCH PASSES
Finally, you can run gate-level static timing analysis.
cd glsta
make
The design must still meet timing, i.e. have a positive slack.
Path 1: MET Setup Check with Pin Xr_reg[31]/CK
Endpoint: Xr_reg[31]/D (^) checked with leading edge of 'clk'
Beginpoint: T_reg[2]/Q (v) triggered by leading edge of 'clk'
Path Groups: {clk}
Other End Arrival Time 0.104
- Setup 0.113
+ Phase Shift 8.000
= Required Time 7.991
- Arrival Time 7.641
= Slack Time 0.350
Clock Rise Edge 0.000
+ Clock Network Latency (Prop) 0.104
= Beginpoint Arrival Time 0.104
----------------------------------------------------------------
Instance Arc Cell Delay Arrival Required
Time Time
----------------------------------------------------------------
T_reg[2] CK ^ - - 0.104 0.454
T_reg[2] CK ^ -> Q v DFFHQX1 0.262 0.366 0.716
g37105 A v -> Y ^ NAND2X1 0.060 0.426 0.776
g36792 C ^ -> Y v NAND3BXL 0.143 0.568 0.919
g36636 A v -> Y ^ NAND3X1 0.136 0.705 1.055
g37800 B0 ^ -> Y v OAI21X1 0.098 0.803 1.153
g36385__2802 B0 v -> Y ^ OAI21X1 0.065 0.868 1.218
g36369__2883 B0 ^ -> Y v AOI2BB1X1 0.073 0.942 1.292
g36293__4319 A2 v -> Y ^ OAI31X1 0.143 1.084 1.434
g36290__2398 A2 ^ -> Y v AOI31X1 0.245 1.329 1.680
g36289__5477 A v -> Y ^ NAND3X1 0.148 1.477 1.827
g36288__6417 A ^ -> Y v NAND2X1 0.123 1.601 1.951
FE_OFC7_n_938 A v -> Y v CLKBUFX6 0.203 1.804 2.154
g36287 A v -> Y ^ CLKINVX6 0.153 1.957 2.307
g36196__2883 B ^ -> Y ^ MX2X1 0.254 2.211 2.561
g36013__5477 B0 ^ -> Y v AOI2BB1X1 0.075 2.286 2.636
g35937__6131 B v -> Y ^ NOR2X1 0.082 2.368 2.719
g35874__1705 A1 ^ -> Y v OAI21X1 0.131 2.500 2.850
g35847__6131 A1 v -> Y ^ AOI21X1 0.130 2.630 2.980
g35816__5115 B0 ^ -> Y v AOI2BB1X1 0.085 2.715 3.065
g35809__2802 B v -> Y ^ NOR2X1 0.089 2.803 3.153
g35792__2883 B0 ^ -> Y v AOI2BB1X1 0.087 2.890 3.240
g35790__9315 B v -> Y ^ NOR2X1 0.084 2.974 3.325
g35758__2883 A1 ^ -> Y v OAI21X1 0.130 3.105 3.455
g35730__5477 A1 v -> Y ^ AOI22X1 0.158 3.263 3.613
g35704__6783 A1 ^ -> Y v OAI21X1 0.165 3.428 3.778
g35674__1705 A1 v -> Y ^ AOI21X1 0.140 3.567 3.917
g35655__2883 A1 ^ -> Y v OAI21X1 0.163 3.730 4.080
g37644 B0 v -> Y v OA21X1 0.149 3.879 4.229
g35620__5107 B v -> Y ^ NOR2X1 0.074 3.953 4.303
g35597__5122 B0 ^ -> Y v AOI2BB1X1 0.083 4.037 4.387
g35595__2802 B v -> Y ^ NOR2X1 0.083 4.120 4.470
g35573__4733 A1 ^ -> Y v OAI21X1 0.150 4.270 4.620
g35548__6417 B1 v -> Y ^ AOI22X1 0.161 4.431 4.781
g35520__8428 B0 ^ -> Y v AOI2BB1X1 0.110 4.541 4.891
g35518__6260 B v -> Y ^ NOR2X1 0.105 4.645 4.996
g35488__6783 A1 ^ -> Y v OAI21X1 0.157 4.803 5.153
g35466__1881 B v -> Y ^ NAND2X1 0.102 4.905 5.255
g35454__4319 B ^ -> Y v NOR2X1 0.069 4.974 5.324
g35428__3680 B1 v -> Y ^ AOI221X1 0.175 5.148 5.499
g35401__5115 A1 ^ -> Y v OAI21X1 0.204 5.352 5.702
g35378 A v -> Y ^ INVX1 0.108 5.461 5.811
g35365__9315 A1 ^ -> Y v OAI21X1 0.123 5.584 5.934
g35350 A v -> Y ^ INVX1 0.102 5.685 6.036
g35339__4319 A1 ^ -> Y v OAI21X1 0.098 5.784 6.134
g35336 A v -> Y ^ INVX1 0.075 5.859 6.209
g35323__6161 A1 ^ -> Y v OAI21X1 0.113 5.972 6.323
g35299__5107 B v -> Y ^ NAND2X1 0.108 6.080 6.430
g35287__6161 A1 ^ -> Y v OAI21X1 0.124 6.204 6.554
g35281 A v -> Y ^ INVX1 0.093 6.297 6.647
g35253__9315 A1 ^ -> Y v OAI21X1 0.109 6.406 6.756
g35238__1617 A1 v -> Y ^ AOI22X1 0.158 6.564 6.914
g35214__6161 A1 ^ -> Y v OAI22X1 0.188 6.752 7.102
g37699 CI v -> CO v ADDFX1 0.245 6.996 7.346
g35194 A v -> Y ^ INVX1 0.072 7.068 7.418
g35184__2883 A1 ^ -> Y v OAI22X2 0.141 7.210 7.560
g35170__5122 B v -> Y v XNOR2X1 0.181 7.391 7.741
g35163__6783 A1 v -> Y ^ AOI21X1 0.078 7.469 7.819
g35160__8428 B0 ^ -> Y v OAI21X1 0.103 7.573 7.923
g35158__4319 B0 v -> Y ^ OAI2BB1X1 0.069 7.641 7.991
Xr_reg[31] D ^ DFFX2 0.000 7.641 7.991
Performance Metrics
The performance metrics used in this lab differ slightly from the convention we have adopted in Lecture 8.
When you optimize for area, the final area of your design is the core area as reported by the
run_innovus.tclscript.When you optimize for throughput, your final throughput is the maximum clock frequency achieved by your design times the number of clock cycles per output. For example, the sample RTL implementation has a cycle budget of 22 cycles and a maximum clock frequency of 125MHz, so the throughput of this design is 5.682 million CORDIC evaluations per second.
The differences of these metrics with our earlier convention is as follows: To define area, we use physical core area, while previously we have used the active area (the area of the standard cells). To define throughput, we determine the clock frequency through the clock period constraint you use for your design, and not the critical path.
Grading Rubric
The lab receives 100 points, to be distributed as follows.
20 points for the RTL design: correctness and quality of the code and the testbench
20 points for the synthesis result: design synthesizes correctly (no latches), meets advertised timing, meets input/output specification
20 points for the layout: design has a layout that meets timing, that has no design violations
20 points for the rank of your design within the category you choose to optimize for (area/throughput). The rank-1 design gets 20 points, the rank-2 design gets 18 points, and so on.
20 points for your report: clearly document your design process, include listings, include tables with area and critical path, include a snapshot of the layout.
Attention
The following are important report requirements.
Use a typesetting tool such as latex or word. Do not submit handwritten scanned reports.
Use a screen capture tool to collect graphics such as layout information. Do not use your smartphone to take a picture from the screen.
Be clear and complete in your report. I am not looking for the correct solution; I am looking to understand your solution. Explain the steps that lead up to a result. The report does not have a minimum length nor a maximum length, as long as it is clear what you did and your answers to questions are complete.
Make sure to update, commit and push the results of your lab to your repository. You do not have to turn in anything on Canvas. All results will be communicated through your github repository.